Question

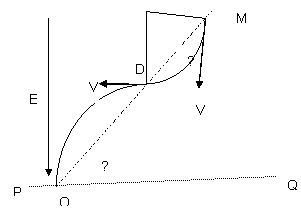
如图所示，虚线MO与水平线PQ相交于O，二者夹角θ=30°，在MO左侧存在电场强度为E、方向竖直向下的匀强电场，MO右侧某个区域存在磁感应强度为B、垂直纸面向外的匀强磁场.现有一个质量为m、电荷量为+q的带电粒子在纸面内以速度v=，且方向与MO成θ角从M点射入磁场,又向左从MO上的D点(图中未画出)射出磁场进入电场，最后到达O点,不计粒子的重力求：

（1）MD的距离L

（2）粒子自M点射入磁场至到达O点所用的时间.

（3）磁场区域的最小面积.

Answer 1

解析：（1）粒子的运动轨迹如图所示，设粒子在匀强磁场中做匀速圆周运动的半径为R 

则 

由几何关系得    L = 2RsinѲ    

又          v=     

由以上三式解得      L =    

 （2）设粒子在匀强磁场中做匀速圆周运动的周期为T，粒子在匀强磁场中运动时间为t₁

    

      

由对称性可知,粒子过MO后方向垂直于电场方向,所以粒子做类平抛运动，设运动的时间为，

则：          x=v

       

又y= x tanѳ

则粒子自M进入磁场至O所用的时间 

解以上各式得： t=      

（3）由题知，磁场范围的最小面积是粒子在磁场中的轨迹与MD所围成的面积。

扇形的面积        

三角形的面积为：    

又               

联立得：或