题目内容
 氢原子能级如图所示,氢原子基态能量E1=-13.6eV,氢的核外电子的第一条可能轨道的半径为r1=0.53×10-10m..氢的核外电子的第n条可能轨道的半径为rn=n2r1求氢原子处于n=4激发态时:(电子的质量m=0.9×10-30kg) 1)电子在轨道上运动的动能;2)电子具有的电势能;(以上各问题结果均保留两位有效数字,能量值以电子伏为单位)
氢原子能级如图所示,氢原子基态能量E1=-13.6eV,氢的核外电子的第一条可能轨道的半径为r1=0.53×10-10m..氢的核外电子的第n条可能轨道的半径为rn=n2r1求氢原子处于n=4激发态时:(电子的质量m=0.9×10-30kg) 1)电子在轨道上运动的动能;2)电子具有的电势能;(以上各问题结果均保留两位有效数字,能量值以电子伏为单位)分析:(1)根据库仑引力提供电子做圆周运动的向心力,求出电子在轨道上的动能.
(2)原子的能量等于电势能和电子动能之和,求出原子在n=4激发态的能量,从而求出电子具有的电势能.
(2)原子的能量等于电势能和电子动能之和,求出原子在n=4激发态的能量,从而求出电子具有的电势能.
解答:解:(1)由k
=m
得,
EK4=
mv2=
.
又r4=16r1
所以EK4=
=
J=0.85eV.
(2)E4=
=
=-0.85eV
所以电子具有的电势能E′=E-EK4=-0.85-0.85eV=-1.7eV.
答:(1)电子在轨道上的动能为0.85eV.
(2)电子具有的电势能为-1.7eV.
| e2 |
| r42 |
| v2 |
| r4 |
EK4=
| 1 |
| 2 |
| 1 |
| 2 |
| ke2 |
| r4 |
又r4=16r1
所以EK4=
| ke2 |
| 32r1 |
| 9×109×(1.6×10-19)2 |
| 32×0.53×10-10 |
(2)E4=
| E1 |
| n2 |
| -13.6eV |
| 16 |
所以电子具有的电势能E′=E-EK4=-0.85-0.85eV=-1.7eV.
答:(1)电子在轨道上的动能为0.85eV.
(2)电子具有的电势能为-1.7eV.
点评:解决本题的关键知道原子的能量等于电势能与电子动能之和,会通过库仑引力提供向心力求出电子的动能.

练习册系列答案
相关题目
 (2006?广州一模)氢原子能级如图所示,一群原处于n=4 能级的氢原子回到n=1的状态过程中( )
(2006?广州一模)氢原子能级如图所示,一群原处于n=4 能级的氢原子回到n=1的状态过程中( ) 一个处于基态的氢原子射向另一个处于基态的静止的氢原子发生碰撞并连成一体,损失的动能使其中的一个氢原子跃迁到激发态,这个氢原子最多能发出两个不同频率的光子.已知:元电荷e=1.6×10-19C,真空中光速c=3.0×108m/s,普朗克常量h=6.63×10-34Js,光子的动量可以不计,氢原子能级如图所示.求:
一个处于基态的氢原子射向另一个处于基态的静止的氢原子发生碰撞并连成一体,损失的动能使其中的一个氢原子跃迁到激发态,这个氢原子最多能发出两个不同频率的光子.已知:元电荷e=1.6×10-19C,真空中光速c=3.0×108m/s,普朗克常量h=6.63×10-34Js,光子的动量可以不计,氢原子能级如图所示.求: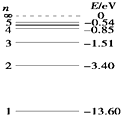 氢原子能级如图所示,则要使一个处于基态的氢原子释放出一个电子而变成为氢离子,该氢原子需要吸收的能量至少是
氢原子能级如图所示,则要使一个处于基态的氢原子释放出一个电子而变成为氢离子,该氢原子需要吸收的能量至少是 (2013?太原一模)在探究光电效应的实验中,用光照射某种金属,测得该金属表面有光电子逸出的最大入射光波长为λ0.若用氢原子发出的光照射该金属,已知氢原子从能级3跃迁到能级2时发出的光可使该金属发生光电效应,但从能级4跃迁到能级3发出的光不能使该金属发生光电效应.已知氢原子能级如图所示,真空中的光速为c.则 ( )
(2013?太原一模)在探究光电效应的实验中,用光照射某种金属,测得该金属表面有光电子逸出的最大入射光波长为λ0.若用氢原子发出的光照射该金属,已知氢原子从能级3跃迁到能级2时发出的光可使该金属发生光电效应,但从能级4跃迁到能级3发出的光不能使该金属发生光电效应.已知氢原子能级如图所示,真空中的光速为c.则 ( )