题目内容
一个倾角为θ=37°的斜面固定在水平面上，一个质量为m=1.0 kg的小物块（可视为质点）以
m/s的初速度由底端沿斜面上滑，小物块与斜面的动摩擦因数
。若斜面足够长，已知
，
，g取10m/s2，求：
（1）小物块沿斜面上滑时的加速度大小；
（2）小物块上滑的最大距离；
（3）小物块返回斜面底端时的速度大小。
m/s的初速度由底端沿斜面上滑，小物块与斜面的动摩擦因数。若斜面足够长，已知，，g取10m/s2，求：（1）小物块沿斜面上滑时的加速度大小；
（2）小物块上滑的最大距离；
（3）小物块返回斜面底端时的速度大小。
解：（1）小物块在斜面上的受力情况如图所示，
重力的分力
根据牛顿第二定律有：
①
②
又因为
③
由①②③式得
④
（2）小物块沿斜面上滑做匀减速运动，到达最高点时速度为零，则有
⑤
⑥
（3）小物块在斜面上的受力情况如图所示，
根据牛顿第二定律有
⑦
⑧
由③⑦⑧式得
⑨
因为
⑩
所以
（或2.8m/s）。
重力的分力
根据牛顿第二定律有：
① ② 又因为
③ 由①②③式得
④ （2）小物块沿斜面上滑做匀减速运动，到达最高点时速度为零，则有
⑤ ⑥ （3）小物块在斜面上的受力情况如图所示，
根据牛顿第二定律有
⑦ ⑧ 由③⑦⑧式得
⑨ 因为
⑩所以
（或2.8m/s）。 
练习册系列答案
课堂全解字词句段篇章系列答案
步步高口算题卡系列答案
相关题目
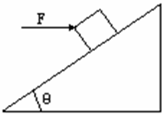一个倾角为37°的斜面固定不动，其上有一个重10N的物体静止不动，当给物体加一个水平向右的从零逐渐增大到8N的推力作用时物体仍不动下列说法正确的是（ ）
一质量为m的物体以某一速度冲上一个倾角为37°的斜面，其运动的加速度的大小为0.9g，这个物体沿斜面上升的最大高度为H，则在这过程中（ ）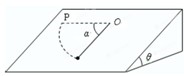
如图所示，在一个倾角为θ=37°（cos37°=0.8）的斜面上，O点固定一根细绳，细绳另一端连接一个质点．现将质点放到斜面上P点，由静止释放，已知OP连线水平且间距为绳长，质点滑动到细绳转过角度α=90°的位置时刚好停止．问：
有一个倾角为37°的固定斜面，斜面长l=3.2m，现将一个质量m=1.0kg的物体放在斜面顶端，对物体施加一个沿斜面向上的恒力F作用F=2.4N．物体从静止开始沿斜面匀加速下滑，经过时间2s，物体恰好滑至斜面底端．