题目内容
 (2012?丰台区模拟)质谱仪原理如图所示,a为粒子加速器,加速电压为U1;b为速度选择器,磁场与电场正交,磁感应强度为B1,板间距离为d;c为偏转分离器,磁感应强度为B2.今有一质量为m,电荷量为+q的带电粒子,经加速后,该粒子恰能沿直线通过速度选择器.粒子从O点进入分离器后在洛伦兹方的作用下做半个圆周运动后打到底片上并被接收,形成一个细条纹,测出条纹到O点的距离为L.求:
(2012?丰台区模拟)质谱仪原理如图所示,a为粒子加速器,加速电压为U1;b为速度选择器,磁场与电场正交,磁感应强度为B1,板间距离为d;c为偏转分离器,磁感应强度为B2.今有一质量为m,电荷量为+q的带电粒子,经加速后,该粒子恰能沿直线通过速度选择器.粒子从O点进入分离器后在洛伦兹方的作用下做半个圆周运动后打到底片上并被接收,形成一个细条纹,测出条纹到O点的距离为L.求:(1)粒子离开加速器的速度大小v?
(2)速度选择器的电压U2?
(3)该带电粒子荷质比
| q | m |
分析:(1)根据动能定理qU1=
mv2求出粒子的速度v.
(2)在速度选择器中作匀速直线运动,电场力与洛仑兹力平衡,根据Eq=qvB1求出电压U2.
(3)根据洛仑兹力提供向心力,qvB2=m
,求出粒子在B2磁场中做匀速圆周运动的半径R.
| 1 |
| 2 |
(2)在速度选择器中作匀速直线运动,电场力与洛仑兹力平衡,根据Eq=qvB1求出电压U2.
(3)根据洛仑兹力提供向心力,qvB2=m
| v2 |
| R |
解答:解:(1)粒子经加速电场U1加速,获得速度V,由动能定理得:
qU1=
mv2 解得v=
故粒子的速度为
.
(2)在速度选择器中作匀速直线运动,电场力与洛仑兹力平衡得
Eq=qvB1即
q=qvB1
U2=B1dv=B1d
故速度选择器的电压U2为B1d
.
(3)在B2中作圆周运动,洛仑兹力提供向心力,有qvB2=m
,
R=
=
.
又R=
,
由以上两式,解得:
=
答:(1)粒子离开加速器的速度大小为
;
(2)速度选择器的电压为B1d
.;
(3)该带电粒子荷质比
的表达式为得:
=
.
qU1=
| 1 |
| 2 |
|
故粒子的速度为
|
(2)在速度选择器中作匀速直线运动,电场力与洛仑兹力平衡得
Eq=qvB1即
| U2 |
| d |
U2=B1dv=B1d
|
故速度选择器的电压U2为B1d
|
(3)在B2中作圆周运动,洛仑兹力提供向心力,有qvB2=m
| v2 |
| R |
R=
| mv |
| qB2 |
| m |
| qB2 |
|
又R=
| L |
| 2 |
由以上两式,解得:
| q |
| m |
| 8U1 | ||
|
答:(1)粒子离开加速器的速度大小为
|
(2)速度选择器的电压为B1d
|
(3)该带电粒子荷质比
| q |
| m |
| q |
| m |
| 8U1 | ||
|
点评:解决本题的关键掌握动能定理,以及知道在速度选择器中作匀速直线运动,电场力与洛仑兹力平衡.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 (2012?丰台区二模)如图所示,在平面xOy内有一沿x轴正方向传播的简谐横波,波速为3.0m/s,频率为2.5Hz,A、B两点位于x轴上,相距0.90m.分别以A、B为平衡位置的两个质元在振动过程中,取A点的质元位于波峰时为t=0,对于B点的质元来说( )
(2012?丰台区二模)如图所示,在平面xOy内有一沿x轴正方向传播的简谐横波,波速为3.0m/s,频率为2.5Hz,A、B两点位于x轴上,相距0.90m.分别以A、B为平衡位置的两个质元在振动过程中,取A点的质元位于波峰时为t=0,对于B点的质元来说( )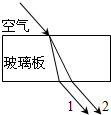 (2012?丰台区一模)频率不同的两束单色光1和2以相同的入射角从同一点射入一厚玻璃板后,其光路如图所示.下列说法正确的是( )
(2012?丰台区一模)频率不同的两束单色光1和2以相同的入射角从同一点射入一厚玻璃板后,其光路如图所示.下列说法正确的是( ) (2012?丰台区一模)图中K、L、M为静电场中的3个相距很近的等势面(K、M之间无电荷).一带电粒子射入此静电场中后,依abcde轨迹运动.已知电势?K<?L<?M,且粒子在ab段做减速运动.下列说法中正确的是( )
(2012?丰台区一模)图中K、L、M为静电场中的3个相距很近的等势面(K、M之间无电荷).一带电粒子射入此静电场中后,依abcde轨迹运动.已知电势?K<?L<?M,且粒子在ab段做减速运动.下列说法中正确的是( )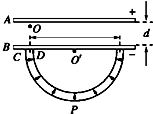 (2012?丰台区二模)如图所示,A、B为两块平行金属板,A板带正电、B板带负电.两板之间存在着匀强电场,两板间距为d、电势差为U,在B板上开有两个间距为L的小孔.C、D为两块同心半圆形金属板,圆心都在贴近B板的O′处,C带正电、D带负电.两板间的距离很近,两板末端的中心线正对着B板上的小孔,两板间的电场强度可认为大小处处相等,方向都指向O′.半圆形金属板两端与B板的间隙可忽略不计.现从正对B板小孔紧靠A板的O处由静止释放一个质量为m、电量为q的带正电微粒(微粒的重力不计),问:
(2012?丰台区二模)如图所示,A、B为两块平行金属板,A板带正电、B板带负电.两板之间存在着匀强电场,两板间距为d、电势差为U,在B板上开有两个间距为L的小孔.C、D为两块同心半圆形金属板,圆心都在贴近B板的O′处,C带正电、D带负电.两板间的距离很近,两板末端的中心线正对着B板上的小孔,两板间的电场强度可认为大小处处相等,方向都指向O′.半圆形金属板两端与B板的间隙可忽略不计.现从正对B板小孔紧靠A板的O处由静止释放一个质量为m、电量为q的带正电微粒(微粒的重力不计),问: