Question

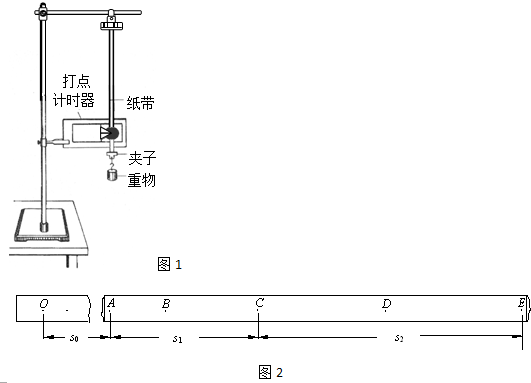
用如图 1所示的实验装置测量物体沿斜面匀加速下滑的加速度，打点计时器打出的纸带如图2所示．已知纸带上各相邻点的时间间隔为T，则可以得出打点计时器在打出C点时小车的速度大小的表达式为

s2+s3

2T

，小车运动的加速度大小的表达式

(s4+s3)-(s1+s2)

4T2

．若测出斜面的长度L和斜面右端距桌面的高度h，已知重力加速度为g，小车的质量为m．则可以得出斜面对小车的阻力的表达式为

mg

h

L

-m

(s3+s4)-(s1+s2)

4T2

．

Answer 1

分析：做匀变速直线运动的物体在某段时间内的平均速度等于该段时间中间时刻的瞬时速度；在相邻的相等时间间隔内的位移差是定值，△x=aT²，据此求出瞬时速度与加速度，根据牛顿第二定律可以求出阻力的表达式．

解答：解：做匀变速直线运动的物体在某段时间内的平均速度等于该段时间中间时刻的瞬时速度，故打C点速度为：
v_C=

s2+s3

2T

；
根据相邻的相等时间间隔内的位移差是定值，即△x=aT²，得：
s3-s1=2a1T2
s4-s2=2a2T2
a=

a1+a2

2

=

(s4+s3)-(s1+s2)

4T2

；
根据牛顿第二定律有：
mgsinθ-f=ma
sinθ=

h

L

联立解得：f=mg

h

L

-m

(s3+s4)-(s1+s2)

4T2

故答案为：

s2+s3

2T

；

(s4+s3)-(s1+s2)

4T2

；mg

h

L

-m

(s3+s4)-(s1+s2)

4T2

．

点评：本题考查了求瞬时速度与加速度问题，熟练应用匀变速运动的推论即可正确解题．