题目内容
1.汽车正以v1=12m/s的速度在平直的公路上匀速行驶,突然发现正前方相距x处有一辆自行车以v2=4m/s的速度同方向匀速行驶,汽车立即以加速度大小a=2m/s2做匀减速直线运动,结果汽车恰好未追上自行车,求x的大小.
分析 汽车与自行车恰好不碰撞的临界情况是速度相等时,恰好不碰撞,结合速度时间公式和位移公式,求出两车相距的距离s.
解答 解:汽车速度和自行车速度相等经历的时间t=$\frac{{v}_{2}-{v}_{1}}{a}=\frac{4-12}{-2}s=4s$,
则x=$\frac{{{v}_{2}}^{2}-{{v}_{1}}^{2}}{2a}-{v}_{2}t$=$\frac{16-144}{2×(-2)}-4×4m$=16m.
答:x的大小为16m.
点评 速度大者减速追速度小者,速度相等前,两者的距离逐渐减小,若不相撞,速度相等后,两者的距离逐渐增大,知临界情况是速度相等时,恰好不相撞.

练习册系列答案
相关题目
9.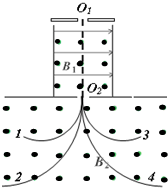 阿尔法磁谱仪主要用于探索宇宙中的反物质,反物质是由反粒子组成的.带电粒子和它的反粒子质量相等,带电量相等但电性相反,例如反质子即为${\;}_{-1}^{1}$H.假若使一束质子、反质子、α粒子和反α粒子${\;}_{-2}^{4}$He组成的射线,沿直线O1O2进入匀强磁场B2而形成图示中的4条径迹则( )
阿尔法磁谱仪主要用于探索宇宙中的反物质,反物质是由反粒子组成的.带电粒子和它的反粒子质量相等,带电量相等但电性相反,例如反质子即为${\;}_{-1}^{1}$H.假若使一束质子、反质子、α粒子和反α粒子${\;}_{-2}^{4}$He组成的射线,沿直线O1O2进入匀强磁场B2而形成图示中的4条径迹则( )
 阿尔法磁谱仪主要用于探索宇宙中的反物质,反物质是由反粒子组成的.带电粒子和它的反粒子质量相等,带电量相等但电性相反,例如反质子即为${\;}_{-1}^{1}$H.假若使一束质子、反质子、α粒子和反α粒子${\;}_{-2}^{4}$He组成的射线,沿直线O1O2进入匀强磁场B2而形成图示中的4条径迹则( )
阿尔法磁谱仪主要用于探索宇宙中的反物质,反物质是由反粒子组成的.带电粒子和它的反粒子质量相等,带电量相等但电性相反,例如反质子即为${\;}_{-1}^{1}$H.假若使一束质子、反质子、α粒子和反α粒子${\;}_{-2}^{4}$He组成的射线,沿直线O1O2进入匀强磁场B2而形成图示中的4条径迹则( )| A. | 径迹2的粒子比径迹1的粒子速度大 | |
| B. | 径迹4的粒子与径迹3的粒子在磁场中回旋时间相等 | |
| C. | 3是反α粒子径迹 | |
| D. | 4是反α粒子径迹 |
16.做匀加速直线运动的物体,运动了时间t.在时间t内,以下说法正确的是( )
| A. | 物体的加速度越大,通过的路程一定越长 | |
| B. | 物体的初速度越大,通过的路程一定越长 | |
| C. | 物体的末速度越大,通过的路程一定越长 | |
| D. | 物体的平均速度越大,通过的路程一定越长 |
6.下列说法正确的是( )
| A. | 参考系的选择是任意的,但要尽量使研究问题变简单 | |
| B. | 物体在某一平面内运动,可以建立二维坐标系来研究物体位置的变化 | |
| C. | 若物体的加速度均匀增加,则物体做匀加速直线运动 | |
| D. | 物体做直线运动,位移大小等于路程 |
13.因测试需要,一辆汽车在某雷达测速区沿平直路面从静止开始匀加速一段时间后,又接着做匀减速运动直到最后停止.表中给出了雷达测出的各个时刻对应的汽车速度数值.求:
(1)汽车在运动过程中的最大速度是多少?
(2)汽车在匀加速和匀减速两阶段的加速度a1、a2分别是多少?
(3)汽车在该区域行驶的总位移s是多少?
| 时刻/s | 0 | 1.0 | 2.0 | 3.0 | 4.0 | 5.0 | 6.0 | 7.0 | 8.0 | 9.0 | 10.0 |
| (m•s-2) | 0 | 3.0 | 6.0 | 9.0 | 12.0 | 10.0 | 8.0 | 6.0 | 4.0 | 2.0 | 0 |
(2)汽车在匀加速和匀减速两阶段的加速度a1、a2分别是多少?
(3)汽车在该区域行驶的总位移s是多少?
 如图所示,竖直平面内有两个有界区域Ⅰ和Ⅱ,宽度均为L,竖直虚线是它们的分界线.区域Ⅰ中有垂直纸面向里的匀强磁场,区域Ⅱ中有匀强电场.质量为m、电量为q的带正电的粒子(重力不计)以初速度V0从O点沿水平方向射入磁场,运动到P点(图中未标出)离开磁场并进入电场,离开时速度方向与竖直方向成45°角,粒子经一段时间后到达电场右边界时速度恰好为零,此后再次从P点返问磁场.求:
如图所示,竖直平面内有两个有界区域Ⅰ和Ⅱ,宽度均为L,竖直虚线是它们的分界线.区域Ⅰ中有垂直纸面向里的匀强磁场,区域Ⅱ中有匀强电场.质量为m、电量为q的带正电的粒子(重力不计)以初速度V0从O点沿水平方向射入磁场,运动到P点(图中未标出)离开磁场并进入电场,离开时速度方向与竖直方向成45°角,粒子经一段时间后到达电场右边界时速度恰好为零,此后再次从P点返问磁场.求:
 某同学在“探究弹力和弹簧伸长的关系”实验中,利用得到的弹力F和弹簧总长度L的数据,作出了F-L图象,如图所示,由此可知:
某同学在“探究弹力和弹簧伸长的关系”实验中,利用得到的弹力F和弹簧总长度L的数据,作出了F-L图象,如图所示,由此可知: