题目内容
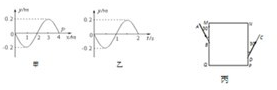
 如图甲所示为一简谐波的波动图象,t=0时,波传播到距波源0.8m的M点,N点是距振源2.0m的一质点.M点的振动图线如图乙所示,求:
如图甲所示为一简谐波的波动图象,t=0时,波传播到距波源0.8m的M点,N点是距振源2.0m的一质点.M点的振动图线如图乙所示,求:(1)简谐波的传播速度;
(2)写出M点的振动方程;
(3)经过多长时间N点通过的路程为0.26m,此时N点的位移为多少?
分析:由波动图象读出波长,由振动图象读出周期,可求出波速.由振动图象上t=0时刻读出质点的速度方向,即可判断出波的传播方向,从而确定M点的振动方程.根据路程与位移的关系,结合周期,即可求解,并由图象可知N质点的位移.
解答:解:(1)由甲图知:波长λ=0.8m,由乙图知:周期T=0.4s,则波速v=
=
m/s=2m/s.
(2)t=0时,波传播到距波源0.8m的M点,而从乙图可知,M的质点此时向下振动,由波的传播方向与质点振动方向的关系知:波沿x轴正向传播.
根据ω
=5πrad/s;M点的振幅为2cm,因此M点的振动方程为y=-2sin5πt(cm);
(3)M质点在一个周期内的路程为S=4A=4×2cm=0.08m;
若N点通过的路程为0.26m,则完成的周期数为
=3
,
即所需要的时间为t1=3
×0.4s=1.3s;
而波传播到N点的时间为t2=
s=0.6s;
因此总时间为t=t1+t2=1.3s+0.6s=1.9s;
所以经过1.9s时间N点通过的路程为0.26m,
波刚传播到N点时,N质点向下振动,经过3
个周期,N质点处于波谷处,则位移为-2cm.
答:(1)简谐波的传播速度2m/s;
(2)写出M点的振动方程y=-2sin5πt(cm);
(3)经过1.9s时间N点通过的路程为0.26m,此时N点的位移为-2cm.
| λ |
| T |
| 0.8 |
| 0.4 |
(2)t=0时,波传播到距波源0.8m的M点,而从乙图可知,M的质点此时向下振动,由波的传播方向与质点振动方向的关系知:波沿x轴正向传播.
根据ω
| 2π |
| T |
(3)M质点在一个周期内的路程为S=4A=4×2cm=0.08m;
若N点通过的路程为0.26m,则完成的周期数为
| 0.26 |
| 0.08 |
| 1 |
| 4 |
即所需要的时间为t1=3
| 1 |
| 4 |
而波传播到N点的时间为t2=
| 2-0.8 |
| 2 |
因此总时间为t=t1+t2=1.3s+0.6s=1.9s;
所以经过1.9s时间N点通过的路程为0.26m,
波刚传播到N点时,N质点向下振动,经过3
| 1 |
| 4 |
答:(1)简谐波的传播速度2m/s;
(2)写出M点的振动方程y=-2sin5πt(cm);
(3)经过1.9s时间N点通过的路程为0.26m,此时N点的位移为-2cm.
点评:本题知道波动图象和质点的振动图象,要把握两种图象之间的内在联系进行分析.

练习册系列答案
相关题目
 如图甲所示为一简谐波在t=0时刻的图象,图乙所示为x=4m处质点P的振动图象,则下列判断正确的是( )
如图甲所示为一简谐波在t=0时刻的图象,图乙所示为x=4m处质点P的振动图象,则下列判断正确的是( )| A、这列波的波速是2m/s | B、这列波的传播方向沿x正方向 | C、t=0.5s时P点的位移为0.2m | D、从t=0时刻开始P点的振动方程为y=0.2sin(πt+π)m |
 【物理-选修3-4】
【物理-选修3-4】
 m
m