题目内容
 如图示是一列向右传播简谐横波在t1时刻的波形,质点P此时的振动速度为V,t2时刻质点P的振动速度与t1时刻的速度大小相等、方向相同;t3时刻质点P的振动速度与t1时刻的速度大小相等、方向相反;已知t2-t1=t3-t2=0.2s,
如图示是一列向右传播简谐横波在t1时刻的波形,质点P此时的振动速度为V,t2时刻质点P的振动速度与t1时刻的速度大小相等、方向相同;t3时刻质点P的振动速度与t1时刻的速度大小相等、方向相反;已知t2-t1=t3-t2=0.2s,求:此波的最小传播速度.
分析:根据波的周期性,得到t2-t1与周期的关系,得出周期的通项.由图读出波长,求出波速的通项,再由数学知识求出波速的最小值.
解答: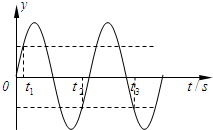 解:因波向右传播,所以质点P从t1时刻开始背离平衡位置振动,
解:因波向右传播,所以质点P从t1时刻开始背离平衡位置振动,
在一个周期内,从t1时刻到t2时刻,从t2时刻t3时刻对应的振动图象如图,则有:
t2-t1=(n+
)T(n=0、1、2…)
所以周期为
T=
(n=0、1、2…)
由图知波长为λ=4m
所以波速为
v=
=5(4n+3)(n=0、1、2…)
当n=0时,波速最小,即最小波速为15m/s.
答:此波的最小传播速度为15m/s.
 解:因波向右传播,所以质点P从t1时刻开始背离平衡位置振动,
解:因波向右传播,所以质点P从t1时刻开始背离平衡位置振动,在一个周期内,从t1时刻到t2时刻,从t2时刻t3时刻对应的振动图象如图,则有:
t2-t1=(n+
| 3 |
| 4 |
所以周期为
T=
| 4(t2-t1) |
| 4n+3 |
由图知波长为λ=4m
所以波速为
v=
| λ |
| T |
当n=0时,波速最小,即最小波速为15m/s.
答:此波的最小传播速度为15m/s.
点评:本题解答关键是抓住波的周期性,即重复性,得出周期的通项.若波的传播方向未知,还考虑波的双向性.

练习册系列答案
相关题目
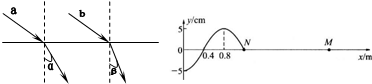

 ,求:此波的最小传播速度。
,求:此波的最小传播速度。 
