题目内容
如图所示,长木板A右边固定着一个挡板,包括挡板在内的总质量为1.5M,静止在光滑的水平地面上.小木块B质量为M,从A的左端开始以初速度v在A上滑动,滑到右端与挡板发生碰撞,已知碰撞过程时间极短,碰后木块B恰好滑到A的左端就停止滑动.已知B与A间的动摩擦因数为μ,B在A板上单程滑行长度为l.求:(1)若μl=
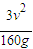 ,在B与挡板碰撞后的运动过程中,摩擦力对木板A做正功还是负功?做多少功?
,在B与挡板碰撞后的运动过程中,摩擦力对木板A做正功还是负功?做多少功?(2)讨论A和B在整个运动过程中,是否有可能在某一段时间里运动方向是向左的.如果不可能,说明理由;如果可能,求出发生这种情况的条件.

【答案】分析:(1)在整个过程中A、B组成的系统动量守恒,应用动量守恒定律与能量守恒定律可以求出摩擦力对A做的功.
(2)分析A、B的运动过程,然后判断它们是否可能向左运动.
解答:解:(1)B与A碰撞后,B相对于A向左运动,A所受摩擦力方向向左,A的运动方向向右,故摩擦力做负功.
设B与A碰撞后的瞬间A的速度为v1,B的速度为v2,A、B相对静止后的共同速度为v,
整个过程中A、B组成的系统动量守恒,由动量守恒定律得:Mv=(M+1.5M)v,解得:v=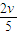 .
.
碰撞后直至相对静止的过程中,系统动量守恒,机械能的减少量等于系统克服摩擦力做的功,
由动量守恒定律得:Mv2+1.5Mv1=2.5Mv,①,由能量守恒定律得: ×1.5Mv12+
×1.5Mv12+ Mv22-
Mv22- ×2.5Mv2=Mμgl ②,
×2.5Mv2=Mμgl ②,
解得:v1= v(另一解v1=
v(另一解v1=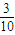 v因小于v而舍去)
v因小于v而舍去)
这段过程中,A克服摩擦力做功:W= ×1.5Mv12-
×1.5Mv12- ×1.5Mv2=
×1.5Mv2=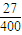 Mv2.
Mv2.
(2)A在运动过程中不可能向左运动,因为在B未与A碰撞之前,A受到的摩擦力方向向右,做加速运动,
碰撞之后A受到的摩擦力方向向左,做减速运动,直到最后,速度仍向右,因此不可能向左运动.
B在碰撞之后,有可能向左运动,即v2<0.
先计算当v2=0时满足的条件,由①式,得
v1=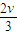 -
-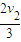 ,当v2=0时,v1=
,当v2=0时,v1=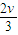 ,代入②式,
,代入②式,
得 ×1.5M
×1.5M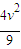 -
- ×2.5M
×2.5M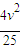 =Mμgl,
=Mμgl,
解得μgl=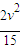 .
.
B在某段时间内向左运动的条件是μl<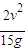 .
.
答:(1)摩擦力对木板A做负功,做的功是-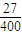 Mv2.
Mv2.
(2)A不可能向左运动,B可能向左运动,B向左运动的条件是:μl<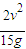 .
.
点评:分析清楚物体的运动过程、应用动量守恒定律与能量守恒定律即可正确解题.
(2)分析A、B的运动过程,然后判断它们是否可能向左运动.
解答:解:(1)B与A碰撞后,B相对于A向左运动,A所受摩擦力方向向左,A的运动方向向右,故摩擦力做负功.
设B与A碰撞后的瞬间A的速度为v1,B的速度为v2,A、B相对静止后的共同速度为v,
整个过程中A、B组成的系统动量守恒,由动量守恒定律得:Mv=(M+1.5M)v,解得:v=
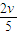 .
.碰撞后直至相对静止的过程中,系统动量守恒,机械能的减少量等于系统克服摩擦力做的功,
由动量守恒定律得:Mv2+1.5Mv1=2.5Mv,①,由能量守恒定律得:
 ×1.5Mv12+
×1.5Mv12+ Mv22-
Mv22- ×2.5Mv2=Mμgl ②,
×2.5Mv2=Mμgl ②,解得:v1=
 v(另一解v1=
v(另一解v1=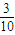 v因小于v而舍去)
v因小于v而舍去)这段过程中,A克服摩擦力做功:W=
 ×1.5Mv12-
×1.5Mv12- ×1.5Mv2=
×1.5Mv2=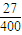 Mv2.
Mv2.(2)A在运动过程中不可能向左运动,因为在B未与A碰撞之前,A受到的摩擦力方向向右,做加速运动,
碰撞之后A受到的摩擦力方向向左,做减速运动,直到最后,速度仍向右,因此不可能向左运动.
B在碰撞之后,有可能向左运动,即v2<0.
先计算当v2=0时满足的条件,由①式,得
v1=
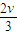 -
-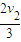 ,当v2=0时,v1=
,当v2=0时,v1=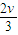 ,代入②式,
,代入②式,得
 ×1.5M
×1.5M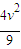 -
- ×2.5M
×2.5M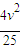 =Mμgl,
=Mμgl,解得μgl=
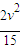 .
.B在某段时间内向左运动的条件是μl<
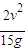 .
.答:(1)摩擦力对木板A做负功,做的功是-
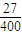 Mv2.
Mv2.(2)A不可能向左运动,B可能向左运动,B向左运动的条件是:μl<
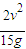 .
.点评:分析清楚物体的运动过程、应用动量守恒定律与能量守恒定律即可正确解题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

 如图所示,长木板A放在光滑的水平地面上,可以看成质点的物块B放在A的左端,已知若B以向右的初速度v0=20m/s从A的左端开始运动,则B滑离A时速度为10m/s,此时A的速度为6m/s,则据此作出的判断正确的是( )
如图所示,长木板A放在光滑的水平地面上,可以看成质点的物块B放在A的左端,已知若B以向右的初速度v0=20m/s从A的左端开始运动,则B滑离A时速度为10m/s,此时A的速度为6m/s,则据此作出的判断正确的是( ) 如图所示,长木板A右边固定着一个挡板,包括挡板在内的总质量为1.5M,静止在光滑的水平地面上.小木块B质量为M,从A的左端开始以初速度v0在A上滑动,滑到右端与档板发生碰撞,已知碰撞过程时间极短,碰后木块B恰好滑到A端就停止滑动,已知B与A间的动摩擦因数为μ,B在A板上单程滑行长度为l,求:
如图所示,长木板A右边固定着一个挡板,包括挡板在内的总质量为1.5M,静止在光滑的水平地面上.小木块B质量为M,从A的左端开始以初速度v0在A上滑动,滑到右端与档板发生碰撞,已知碰撞过程时间极短,碰后木块B恰好滑到A端就停止滑动,已知B与A间的动摩擦因数为μ,B在A板上单程滑行长度为l,求: