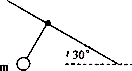题目内容
如图1高空滑索是一项勇敢者的游戏,如果一个质量为70kg的人用轻绳通过轻质滑环悬吊在倾角为θ=30°的足够长的钢索上在重力作用下运动,问:(g=10m/s2)(1)假设轻质滑环与钢索没有摩擦,请扼要说明悬绳与钢索垂直的道理(如图2),并求出人做匀加速运动的加速度.
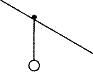
(2)假设轻质滑环与钢索有摩擦而使滑环和人一起做匀速直线运动,请扼要说明悬绳呈竖直方向的道理(如图3),并求出此时滑环与钢索间的动摩擦因数.
(3)在(1)小题情景中,己知悬绳长1m,最大承受力为7800N,当人运动的速度达到lOm/s时,滑环突然卡死,通过计算回答悬绳是否会被拉斯?
【答案】分析:1、以轻质滑环为研究对象,假设悬绳与钢索不垂直,滑环所受合力就不为零,它的加速度可达到无限大,这与事实不符,所以只能垂直.对人进行受力分析,根据牛顿第二定律可求此时人的加速度.
2、以人为研究对象,假设悬绳不竖直,人所受合力就不为零,人就不能做匀速直线运动.所以,悬绳只能竖直方向.对滑环进行受力分析,根据牛顿第二定律可求滑动摩擦力,进一步可求μ.
3、滑环卡死后,人就绕滑环做圆周运动,在最低点悬绳受到的拉力最大.滑环卡死时,根据机械能守恒求得到达最低点的速度,在最低点时,根据合力提供向心力列式求解此时的绳子中的拉力,跟题目中提供的最大拉力比较即可.
解答:解:(1)以轻质滑环为研究对象,假设悬绳与钢索不垂直,滑环所受合力就不为零,它的加速度可达到无限大,这与事实不符,所以只能垂直.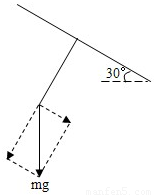
对人进行受力分析,根据牛顿第二定律有
mgsin30°=ma人
所以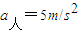
方向沿钢索向下.
(2)以人为研究对象,假设悬绳不竖直,人所受合力就不为零,人就不能做匀速直线运动.
所以,悬绳只能竖直方向
对滑环进行受力分析,根据牛顿第二定律有
∵f=mgsin30°
而f=μN=μmgcos30°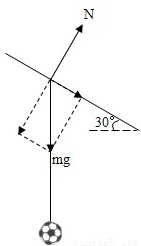
∴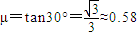
(3)滑环卡死后,人就绕滑环做圆周运动,在最低点悬绳受到的拉力最大.
滑环卡死时人的速度为v=10m/s,在最低点的速度为v,绳长为L=1m,则根据机械能守恒有
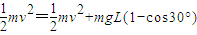
解得v2=102.679(m/s)2
设人在最低点时,绳的拉力为T,则根据合力提供向心力有
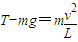
所以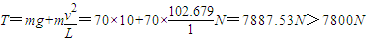
故悬绳会断.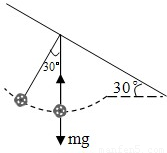
答:(1)假设轻质滑环与钢索没有摩擦,悬绳与钢索是垂直的,道理如上所述,此时人做匀加速运动的加速度为5m/s2.
(2)假设轻质滑环与钢索有摩擦而使滑环和人一起做匀速直线运动,悬绳呈竖直方向,道理如上所述,此时滑环与钢索间的动摩擦因数为0.58.
(3)在(1)小题情景中,己知悬绳长1m,最大承受力为7800N,当人运动的速度达到lOm/s时,滑环突然卡死,通过计算发现悬绳会被拉断.
点评:该题的关键在于能够对不同的问题适时地转换研究对象,特别要注意轻质环是没有质量的,合力不为零是加速度应为无穷大.本题有一点的难度,属于难题.
2、以人为研究对象,假设悬绳不竖直,人所受合力就不为零,人就不能做匀速直线运动.所以,悬绳只能竖直方向.对滑环进行受力分析,根据牛顿第二定律可求滑动摩擦力,进一步可求μ.
3、滑环卡死后,人就绕滑环做圆周运动,在最低点悬绳受到的拉力最大.滑环卡死时,根据机械能守恒求得到达最低点的速度,在最低点时,根据合力提供向心力列式求解此时的绳子中的拉力,跟题目中提供的最大拉力比较即可.
解答:解:(1)以轻质滑环为研究对象,假设悬绳与钢索不垂直,滑环所受合力就不为零,它的加速度可达到无限大,这与事实不符,所以只能垂直.

对人进行受力分析,根据牛顿第二定律有
mgsin30°=ma人
所以
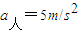
方向沿钢索向下.
(2)以人为研究对象,假设悬绳不竖直,人所受合力就不为零,人就不能做匀速直线运动.
所以,悬绳只能竖直方向
对滑环进行受力分析,根据牛顿第二定律有
∵f=mgsin30°
而f=μN=μmgcos30°

∴
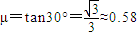
(3)滑环卡死后,人就绕滑环做圆周运动,在最低点悬绳受到的拉力最大.
滑环卡死时人的速度为v=10m/s,在最低点的速度为v,绳长为L=1m,则根据机械能守恒有
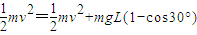
解得v2=102.679(m/s)2
设人在最低点时,绳的拉力为T,则根据合力提供向心力有
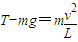
所以
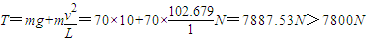
故悬绳会断.

答:(1)假设轻质滑环与钢索没有摩擦,悬绳与钢索是垂直的,道理如上所述,此时人做匀加速运动的加速度为5m/s2.
(2)假设轻质滑环与钢索有摩擦而使滑环和人一起做匀速直线运动,悬绳呈竖直方向,道理如上所述,此时滑环与钢索间的动摩擦因数为0.58.
(3)在(1)小题情景中,己知悬绳长1m,最大承受力为7800N,当人运动的速度达到lOm/s时,滑环突然卡死,通过计算发现悬绳会被拉断.
点评:该题的关键在于能够对不同的问题适时地转换研究对象,特别要注意轻质环是没有质量的,合力不为零是加速度应为无穷大.本题有一点的难度,属于难题.

练习册系列答案
相关题目

 (2009?江门一模)如图1高空滑索是一项勇敢者的游戏,如果一个质量为70kg的人用轻绳通过轻质滑环悬吊在倾角为θ=30°的足够长的钢索上在重力作用下运动,问:(g=10m/s2)
(2009?江门一模)如图1高空滑索是一项勇敢者的游戏,如果一个质量为70kg的人用轻绳通过轻质滑环悬吊在倾角为θ=30°的足够长的钢索上在重力作用下运动,问:(g=10m/s2)