题目内容
某球形天体的密度为ρ0,引力常量为G.
(1)证明对环绕密度相同的球形天体表面运行的卫星,运动周期与天体的大小无关.(球的体积公式为![]() ,其中R为球半径)
,其中R为球半径)
(2)若球形天体的半径为R,自转的角速度为![]() ,表面周围空间充满厚度
,表面周围空间充满厚度![]() (小于同步卫星距天体表面的高度)、密度ρ=
(小于同步卫星距天体表面的高度)、密度ρ=![]() 的均匀介质,试求同步卫星距天体表面的高度.
的均匀介质,试求同步卫星距天体表面的高度.
答案:
解析:
解析:
|
解:(1)设环绕其表面运行卫星的质量为m,运动周期为T,球形天体半径为R,天体质量为M,由牛顿第二定律有 而 由①②式解得 (2)设该天体的同步卫星距天体中心的距离为r,同步卫星的的质量为m0,则有 而 由②③④式解得 则该天体的同步卫星距表面的高度 |

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目
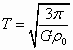 ,可见T与R无关,为一常量.
,可见T与R无关,为一常量. ,其中R为球半径)
,其中R为球半径) ,表面周围空间充满厚度
,表面周围空间充满厚度 (小于同步卫星距天体表面的高度)、密度ρ=
(小于同步卫星距天体表面的高度)、密度ρ= 的均匀介质,试求同步卫星距天体表面的高度.
的均匀介质,试求同步卫星距天体表面的高度.