题目内容
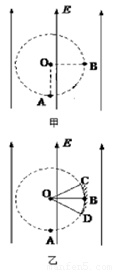
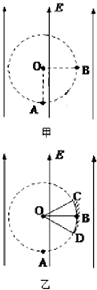 如图甲所示,场强大小为E、方向竖直向上的匀强电场内存在着一半径为R的圆形区域,O点为该圆形区域的圆心,A点是圆形区域的最低点,B点是圆形区域最右侧的点.在A点有放射源释放出初速度大小不同、方向均垂直于场强向右的正电荷,电荷的质量均为m,电量均为q,不计重力.试求:
如图甲所示,场强大小为E、方向竖直向上的匀强电场内存在着一半径为R的圆形区域,O点为该圆形区域的圆心,A点是圆形区域的最低点,B点是圆形区域最右侧的点.在A点有放射源释放出初速度大小不同、方向均垂直于场强向右的正电荷,电荷的质量均为m,电量均为q,不计重力.试求:(1)电荷在电场中运动的加速度多大?
(2)运动轨迹经过B点的电荷在A点时的速度多大?
(3)若在圆形区域的边缘有一圆弧形接收屏CBD,B点仍是圆形区域最右侧的点,C、D分别为接收屏上最边缘的两点,如图乙所示,∠COB=∠BOD=37°.求该屏上接收到的电荷的末动能大小的范围.( 提示:sin37°=0.6,cos37°=0.8.)
分析:(1)根据牛顿第二定律求出电荷在电场中运动的加速度大小.
(2)电荷在电场中做类平抛运动,结合水平位移和竖直位移求出初速度的大小.
(3)结合动能定理和类平抛运动的规律求出从A点运动到圆周上某一点动能的表达式,根据表达式确定出最大动能和最小动能的位置,从而求出该屏上接收到的电荷的末动能大小的范围.
(2)电荷在电场中做类平抛运动,结合水平位移和竖直位移求出初速度的大小.
(3)结合动能定理和类平抛运动的规律求出从A点运动到圆周上某一点动能的表达式,根据表达式确定出最大动能和最小动能的位置,从而求出该屏上接收到的电荷的末动能大小的范围.
解答:解:(1)根据牛顿第二定律得:qE=ma… ①
解得:a=
… ②
(2)电荷在电场中做类平抛运动,设A点的速度为vA,则有:
水平方向:R=vAt…③
竖直方向:R=
at2…④
联立①②③④式得:vA=
…⑤
(3)设圆周上任意一点P与OA成θ角,如甲图,电荷以初速度v0由A运动到P的时间为t0,则
水平方向:Rsinθ=v0t0.
竖直方向:R-Rcosθ=
at02…⑦
A点的动能:EkA=
mv02…⑧
对电荷由A运动到P的过程运用动能定理得:qE(R-Rcosθ)=Ekp-EkA… ⑨
联立②⑥⑦⑧⑨式得:Ekp=
qER(5-3cosθ)…⑩
由⑩可知,θ角增大,Ekp增大,如乙图,因此D点接收到的电荷的末动能最小,C点接收到的电荷的末动能最大.
最小动能为:EkD=
qER(5-3cos53°)=
qER.
最大动能为:Ekc=
qER(5-3cos127°)=
qER.
答:(1)电荷在电场中运动的加速度为
.
(2)运动轨迹经过B点的电荷在A点时的速度大小为vA=
.
(3)该屏上接收到的电荷的末动能大小的范围为[
qER,
qER].

解得:a=
| qE |
| m |
(2)电荷在电场中做类平抛运动,设A点的速度为vA,则有:
水平方向:R=vAt…③
竖直方向:R=
| 1 |
| 2 |
联立①②③④式得:vA=
|
(3)设圆周上任意一点P与OA成θ角,如甲图,电荷以初速度v0由A运动到P的时间为t0,则
水平方向:Rsinθ=v0t0.
竖直方向:R-Rcosθ=
| 1 |
| 2 |
A点的动能:EkA=
| 1 |
| 2 |
对电荷由A运动到P的过程运用动能定理得:qE(R-Rcosθ)=Ekp-EkA… ⑨
联立②⑥⑦⑧⑨式得:Ekp=
| 1 |
| 4 |
由⑩可知,θ角增大,Ekp增大,如乙图,因此D点接收到的电荷的末动能最小,C点接收到的电荷的末动能最大.
最小动能为:EkD=
| 1 |
| 4 |
| 4 |
| 5 |
最大动能为:Ekc=
| 1 |
| 4 |
| 17 |
| 10 |
答:(1)电荷在电场中运动的加速度为
| qE |
| m |
(2)运动轨迹经过B点的电荷在A点时的速度大小为vA=
|
(3)该屏上接收到的电荷的末动能大小的范围为[
| 4 |
| 5 |
| 17 |
| 10 |
点评:本题综合考查了动能定理与类平抛运动的综合,难度中等,第三问对学生要求较高,通过某点动能的通项表达式确定出最大动能位置和最小动能位置.

练习册系列答案
相关题目
 如图甲所示,场强大小为E、方向竖直向上的匀强电场内存在着一半径为R的圆形区域,O点为该圆形区域的圆心,A点是圆形区域的最低点,B点是最右侧的点.在A点有放射源释放出初速度大小不同、方向均垂直于场强向右的正电荷,电荷的质量为m,电量为q,不计重力.试求:
如图甲所示,场强大小为E、方向竖直向上的匀强电场内存在着一半径为R的圆形区域,O点为该圆形区域的圆心,A点是圆形区域的最低点,B点是最右侧的点.在A点有放射源释放出初速度大小不同、方向均垂直于场强向右的正电荷,电荷的质量为m,电量为q,不计重力.试求: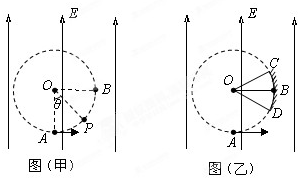 如图甲所示,场强大小为E、方向竖直向上的匀强电场内存在一竖直平面内半径为R的圆形区域,O点为该圆形区域的圆心,A点是圆形区域的最低点,B点是最右侧的点,在A点放射源释放出初速度大小不同、方向均垂直于场强向右的正电荷,电荷的质量为m,电量为q,不计重力.试求:
如图甲所示,场强大小为E、方向竖直向上的匀强电场内存在一竖直平面内半径为R的圆形区域,O点为该圆形区域的圆心,A点是圆形区域的最低点,B点是最右侧的点,在A点放射源释放出初速度大小不同、方向均垂直于场强向右的正电荷,电荷的质量为m,电量为q,不计重力.试求: