题目内容
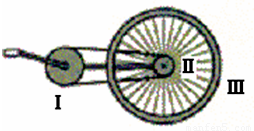 小明同学在学习了圆周运动的知识后,设计了一个课题,名称为:快速测量自行车的骑行速度.他的设想是:通过计算踏脚板转动的角速度,推算自行车的骑行速度.如图是自行车的传动示意图,其中Ⅰ是大齿轮,Ⅱ是小齿轮,Ⅲ是后轮.当大齿轮Ⅰ(脚踏板)的转速通过测量为n(r/s)时,则大齿轮的角速度是 rad/s.若要知道在这种情况下自行车前进的速度,除需要测量大齿轮Ⅰ的半径r1,小齿轮Ⅱ的半径r2外,还需要测量的物理量是 .用上述物理量推导出自行车前进速度的表达式为: .
小明同学在学习了圆周运动的知识后,设计了一个课题,名称为:快速测量自行车的骑行速度.他的设想是:通过计算踏脚板转动的角速度,推算自行车的骑行速度.如图是自行车的传动示意图,其中Ⅰ是大齿轮,Ⅱ是小齿轮,Ⅲ是后轮.当大齿轮Ⅰ(脚踏板)的转速通过测量为n(r/s)时,则大齿轮的角速度是 rad/s.若要知道在这种情况下自行车前进的速度,除需要测量大齿轮Ⅰ的半径r1,小齿轮Ⅱ的半径r2外,还需要测量的物理量是 .用上述物理量推导出自行车前进速度的表达式为: .
【答案】分析:转速的单位为转/秒,即单位时间做圆周运动转过的圈数,转过一圈对应的圆心角为2π,所以角速度ω=转速n×2π,由于大齿轮I和小齿轮II是通过链条传动,所以大小齿轮边缘上线速度大小相等,又小齿轮II和车轮III是同轴转动,所以它们角速度相等,要知道车轮边缘线速度的大小,则需要知道车轮的半径;利用I和II线速度大小相等,II和III角速度相等,列式求III的线速度大小即可.
解答:解:转速为单位时间内转过的圈数,因为转动一圈,对圆心转的角度为2π,所以ω=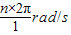 =2πnrad/s,因为要测量自行车前进的速度,即车轮III边缘上的线速度的大小,根据题意知:轮I和轮II边缘上的线速度的大小相等,据v=Rω可知:RIωI=RIIωII,已知ωI=2πn,则轮II的角速度ωII=
=2πnrad/s,因为要测量自行车前进的速度,即车轮III边缘上的线速度的大小,根据题意知:轮I和轮II边缘上的线速度的大小相等,据v=Rω可知:RIωI=RIIωII,已知ωI=2πn,则轮II的角速度ωII=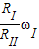 .因为轮II和轮III共轴,所以转动的ω相等即ωIII=ωII,根据v=Rω可知,要知道轮III边缘上的线速度大小,还需知道轮III的半径RIII 其计算式v=RIIIωIII=
.因为轮II和轮III共轴,所以转动的ω相等即ωIII=ωII,根据v=Rω可知,要知道轮III边缘上的线速度大小,还需知道轮III的半径RIII 其计算式v=RIIIωIII=
故答案为:2πn,轮III的半径RIII,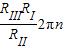
点评:齿轮传动时,轮边缘上的线速度大小相等,同轴转动两轮的角速度相同;转速和角速度的互换问题.
解答:解:转速为单位时间内转过的圈数,因为转动一圈,对圆心转的角度为2π,所以ω=
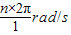 =2πnrad/s,因为要测量自行车前进的速度,即车轮III边缘上的线速度的大小,根据题意知:轮I和轮II边缘上的线速度的大小相等,据v=Rω可知:RIωI=RIIωII,已知ωI=2πn,则轮II的角速度ωII=
=2πnrad/s,因为要测量自行车前进的速度,即车轮III边缘上的线速度的大小,根据题意知:轮I和轮II边缘上的线速度的大小相等,据v=Rω可知:RIωI=RIIωII,已知ωI=2πn,则轮II的角速度ωII=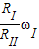 .因为轮II和轮III共轴,所以转动的ω相等即ωIII=ωII,根据v=Rω可知,要知道轮III边缘上的线速度大小,还需知道轮III的半径RIII 其计算式v=RIIIωIII=
.因为轮II和轮III共轴,所以转动的ω相等即ωIII=ωII,根据v=Rω可知,要知道轮III边缘上的线速度大小,还需知道轮III的半径RIII 其计算式v=RIIIωIII=
故答案为:2πn,轮III的半径RIII,
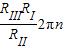
点评:齿轮传动时,轮边缘上的线速度大小相等,同轴转动两轮的角速度相同;转速和角速度的互换问题.

练习册系列答案
相关题目
 小明同学在学习了圆周运动的知识后,设计了一个课题,名称为:快速测量自行车的骑行速度.他的设想是:通过计算踏脚板转动的角速度,推算自行车的骑行速度.如图是自行车的传动示意图,其中Ⅰ是大齿轮,Ⅱ是小齿轮,Ⅲ是后轮.当大齿轮Ⅰ(脚踏板)的转速通过测量为n(r/s)时,则大齿轮的角速度是
小明同学在学习了圆周运动的知识后,设计了一个课题,名称为:快速测量自行车的骑行速度.他的设想是:通过计算踏脚板转动的角速度,推算自行车的骑行速度.如图是自行车的传动示意图,其中Ⅰ是大齿轮,Ⅱ是小齿轮,Ⅲ是后轮.当大齿轮Ⅰ(脚踏板)的转速通过测量为n(r/s)时,则大齿轮的角速度是 小明同学在学习了圆周运动的知识后,设计了一个课题,名称为:快速测量自行车的骑行速度.他的设想是:通过计算踏脚板转动的角速度,推算自行车的骑行速度.经过骑行,他得到如下的数据:在时间t内踏脚板转动的圈数为N,那么踏脚板转动的角速度ω=
小明同学在学习了圆周运动的知识后,设计了一个课题,名称为:快速测量自行车的骑行速度.他的设想是:通过计算踏脚板转动的角速度,推算自行车的骑行速度.经过骑行,他得到如下的数据:在时间t内踏脚板转动的圈数为N,那么踏脚板转动的角速度ω= 小明同学在学习了圆周运动的知识后,设计了一个课题,名称为:快速测量自行车的骑行速度.他的设想是:通过计算踏脚板转动的角速度,推算自行车的骑行速度.经过骑行,他得到如下的数据:
小明同学在学习了圆周运动的知识后,设计了一个课题,名称为:快速测量自行车的骑行速度.他的设想是:通过计算踏脚板转动的角速度,推算自行车的骑行速度.经过骑行,他得到如下的数据:
