题目内容
11.已知万有引力常量,利用下列哪组,可以计算出地球的质量( )| A. | 卫星绕地球做匀速圆周运动的线速度和周期 | |
| B. | 卫星绕地球做匀速圆周运动的轨道半径和周期 | |
| C. | 卫星绕地球做匀速圆周运动的轨道半径和线速度 | |
| D. | 卫星绕地球做匀速圆周运动的周期和角速度 |
分析 计算中心天体质量的主要思路有:一是在星球表面重力与万有引力相等,据重力加速度和地球半径求地球的质量,二是环绕天体围绕地球圆周运动的向心力由万有引力提供,根据圆周运动的物理量可以求中心天体的质量.
解答 解:A、已知卫星绕地球做匀速圆周运动的线速度和周期,根据圆周运动的公式得轨道半径r=$\frac{vT}{2π}$,
由万有引力提供向心力得$\frac{GMm}{{r}^{2}}$=m$\frac{{4π}^{2}}{{T}^{2}}$r,
解得:M=$\frac{{v}^{3}T}{2πG}$,所以可求出地球的质量,故A正确;
B、已知卫星绕地球做匀速圆周运动的轨道半径和周期,
由万有引力提供向心力得$\frac{GMm}{{r}^{2}}$=m$\frac{{4π}^{2}}{{T}^{2}}$r,
M=$\frac{{{4π}^{2}r}^{3}}{{GT}^{2}}$,故B正确;
C、已知卫星绕地球做匀速圆周运动的轨道半径和线速度,
由万有引力提供向心力得
$\frac{GMm}{{r}^{2}}$=m$\frac{{v}^{2}}{r}$,所以可求出地球的质量,故C正确;
D、已知卫星绕地球做匀速圆周运动的周期和角速度,
由万有引力提供向心力得$\frac{GMm}{{r}^{2}}$=m$\frac{{4π}^{2}}{{T}^{2}}$r,
由于不知道轨道半径,所以不能求出地球的质量,故D错误;
故选:ABC.
点评 万有引力应用的主要入手点是星球表面重力与万有引力相等,二是万有引力提供环绕天体的向心力.据此只能计算中心天体的质量.

练习册系列答案
相关题目
1.F1、F2是力F的两个分力.若F=12N,则下列不可能是F的两个分力的是( )
| A. | F1=12 N,F2=12 N | B. | F1=20 N,F2=20 N | C. | F1=15 N,F2=30 N | D. | F1=30 N,F2=40 N |
6.关于库仑定律的公式F=k$\frac{{Q}_{1}{Q}_{2}}{{r}^{2}}$,下列说法中正确的是( )
| A. | 当真空中的两个点电荷间的距离r→∞时,它们之间的静电力F→∞ | |
| B. | 当真空中的两个点电荷间的距离r→0时,它们之间的静电力F→∞ | |
| C. | 当两个点电荷之间的距离r→∞时,库仑定律的公式就不适用了 | |
| D. | 当两个点电荷之间的距离r→0时,电荷不能看成是点电荷,库仑定律的公式就不适用 |
16.一列简谐横波,在t=5.0s时的波形如图甲所示,图乙是这列波中x=200cm处的质点P的振动图线,那么该波的传播速度和传播方向是( )
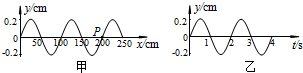
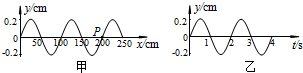
| A. | v=0.25m/s,向右传播 | B. | v=0.50m/s,向左传播 | ||
| C. | v=0.25m/s,向左传播 | D. | v=0.50m/s,向右传播 |
3.物体静止在斜面上,下列说法不正确的是( )
| A. | 物体对斜面的压力和斜面对物体的支持力均属于弹力 | |
| B. | 物体对斜面的摩擦力和斜面对物体的摩擦力是一对平衡力 | |
| C. | 物体所受重力和斜面对物体的作用力是平衡力 | |
| D. | 物体所受重力可以分解为沿斜面向下的力和对斜面的压力 |
1. 两个轻弹簧分别与质量为m的物体相连接,劲度系数分别为k1和k2,装置呈竖直状态静止在水平地面上,如图所示.劲度系数为k2的弹簧与地面不栓接.现用竖直向上的拉力F拉劲度系数为k1的弹簧上端A点,使A点缓慢上升,当下边弹簧的下端即将离开地面时( )
两个轻弹簧分别与质量为m的物体相连接,劲度系数分别为k1和k2,装置呈竖直状态静止在水平地面上,如图所示.劲度系数为k2的弹簧与地面不栓接.现用竖直向上的拉力F拉劲度系数为k1的弹簧上端A点,使A点缓慢上升,当下边弹簧的下端即将离开地面时( )
 两个轻弹簧分别与质量为m的物体相连接,劲度系数分别为k1和k2,装置呈竖直状态静止在水平地面上,如图所示.劲度系数为k2的弹簧与地面不栓接.现用竖直向上的拉力F拉劲度系数为k1的弹簧上端A点,使A点缓慢上升,当下边弹簧的下端即将离开地面时( )
两个轻弹簧分别与质量为m的物体相连接,劲度系数分别为k1和k2,装置呈竖直状态静止在水平地面上,如图所示.劲度系数为k2的弹簧与地面不栓接.现用竖直向上的拉力F拉劲度系数为k1的弹簧上端A点,使A点缓慢上升,当下边弹簧的下端即将离开地面时( )| A. | 物体比施加F前高$\frac{mg}{{k}_{2}}$ | B. | A点比施加F前高$\frac{mg}{{k}_{1}}$ | ||
| C. | F<mg | D. | F>mg |
 如图将筷子竖直插入薄壁玻璃杯内(不在正中央),注水后从俯视图中的P点沿水平方向,看到的应该是下面哪个图中的情形( )
如图将筷子竖直插入薄壁玻璃杯内(不在正中央),注水后从俯视图中的P点沿水平方向,看到的应该是下面哪个图中的情形( )



 质量m=2.5kg的物体静止在粗糙的水平面上,在如图所示的水平拉力F作用下开始运动,则6s末物体的速度大小为多少?(已知物体与水平面间动摩擦因数0.2,g取10m/s2)
质量m=2.5kg的物体静止在粗糙的水平面上,在如图所示的水平拉力F作用下开始运动,则6s末物体的速度大小为多少?(已知物体与水平面间动摩擦因数0.2,g取10m/s2)