题目内容
6. 如图所示,两条平行的光滑金属导轨固定在倾角为θ的绝缘斜面上,导轨上端连接一个定值电阻.导体棒a和b放在导轨上,与导轨垂直并良好接触.斜面上水平虚线PQ以下区域内,存在着垂直穿过斜面向上的匀强磁场.现对a棒施以平行导轨斜向上的拉力,使它沿导轨匀速向上运动,此时放在导轨下端的b棒恰好静止.当a棒运动到磁场的上边界PQ处时,撤去拉力,a棒将继续沿导轨向上运动一小段距离后再向下滑动,此时b棒已滑离导轨.当a棒再次滑回到磁场上边界PQ处时,又恰能沿导轨匀速向下运动.已知a棒、b棒电阻均为2R,定值电阻的阻值为R,b棒的质量为m,重力加速度为g,导轨电阻不计.求:
如图所示,两条平行的光滑金属导轨固定在倾角为θ的绝缘斜面上,导轨上端连接一个定值电阻.导体棒a和b放在导轨上,与导轨垂直并良好接触.斜面上水平虚线PQ以下区域内,存在着垂直穿过斜面向上的匀强磁场.现对a棒施以平行导轨斜向上的拉力,使它沿导轨匀速向上运动,此时放在导轨下端的b棒恰好静止.当a棒运动到磁场的上边界PQ处时,撤去拉力,a棒将继续沿导轨向上运动一小段距离后再向下滑动,此时b棒已滑离导轨.当a棒再次滑回到磁场上边界PQ处时,又恰能沿导轨匀速向下运动.已知a棒、b棒电阻均为2R,定值电阻的阻值为R,b棒的质量为m,重力加速度为g,导轨电阻不计.求:(1)a棒在磁场中沿导轨向上运动的过程中,a棒中的电流Ia与定值电阻R中的电流IR之比;以及a棒质量ma;
(2)a棒在磁场中沿导轨向上运动时所受的拉力F.
分析 (1)由串并联电路的电流规律可得出两电阻中电流之比;对b棒由受力平衡可求得Ib,进而求得Ia;因a棒离开磁场后机械能守恒,故返回磁场时的速度相等,则由返回磁场时做匀速运动可由受力平衡得出a的速度,联立各式可得出a的质量;
(2)已知Ib,则由安培力公式可求得b受到的安培力.
解答 解:(1)a棒为电源,通过a棒的电流为总电流,b棒和电阻R的电阻之比为:2:1,b棒和电阻R等效电阻为:$R′=\frac{2RR}{2R+R}=\frac{2}{3}R$
通过电阻R的电流为总电流的$\frac{2}{3}$,故$\frac{{I}_{a}}{{I}_{R}}=\frac{3}{2}$,同理:$\frac{{I}_{a}}{{I}_{b}}=\frac{3}{1}$
b棒保持静止,则mbgsinθ=BIbL
Ib=$\frac{{m}_{b}gsinθ}{BL}$①
Ia=3Ib ②
a棒脱离磁场后机械能守恒,返回磁场时速度与离开时速度相等,为V,
返回进入磁场时匀速下降,则有:magsinθ=$\frac{{B}^{2}{L}^{2}V}{2R}$
V=$\frac{2R{m}_{a}gsinθ}{{B}^{2}{L}^{2}}$③
A棒匀速上升时 切割磁感线 Ia=$\frac{BLV}{2R+\frac{2}{3}R}$④
由①---④得 ma=4mb=4m
(2)Ia=2Ib
Ib=$\frac{{m}_{b}gsinθ}{BL}$
F=magsinθ+BIaL
b受到的安培力:F=5mgsinθ.
答:(1)a棒在磁场中沿导轨向上运动的过程中,a棒中的电流Ia与定值电阻R中的电流IR之比为3:2;以及a棒质量ma为4m;
(2)a棒在磁场中沿导轨向上运动时所受的拉力F等于5mgsinθ.
点评 电磁感应常常与能量及受力结合,在分析此类问题时要注意物体的运动状态,从而灵活地选择物理规律求解.

 天天练口算系列答案
天天练口算系列答案| A. | 核子结合成原子核吸收的能量或原子核拆解成核子放出的能量称为结合能 | |
| B. | 比结合能越大的原子核越稳定,但它的结合能不一定越大 | |
| C. | 重核与中等质量原子核相比较,重核的结合能和比结合能都大 | |
| D. | 中等质量原子核的结合能和比结合能均比轻核的要大 |
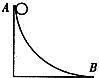 如图所示,物体沿曲面从A点无初速度滑下,滑至曲面的最低点B时,下滑的高度为5m,速度为6m/s,若物体的质量为1kg.则下滑过程中物体克服阻力所做的功为( )
如图所示,物体沿曲面从A点无初速度滑下,滑至曲面的最低点B时,下滑的高度为5m,速度为6m/s,若物体的质量为1kg.则下滑过程中物体克服阻力所做的功为( )| A. | 50J | B. | 18J | C. | 32J | D. | 0J |
| A. | 周期之比T1:T2=3:1 | B. | 线速度之比v1:v2=3:1 | ||
| C. | 向心力之比为F1:F2=1:18 | D. | 向心加速度之比a1:a2=1:9 |
 如图所示,平行放置的金属导轨A、B之间的距离为l,一金属杆长为2l,一端以转轴O固定在导轨B上,并与A无摩擦接触,杆从垂直于导轨的位置,在导轨平面内以角速度ω顺时针匀速转动至另一端落在导轨B上.如两导轨间是一磁感应强度为B,方向垂直于纸面向里的匀强磁场、不计一切电阻,则在上述整个转动过程中( )
如图所示,平行放置的金属导轨A、B之间的距离为l,一金属杆长为2l,一端以转轴O固定在导轨B上,并与A无摩擦接触,杆从垂直于导轨的位置,在导轨平面内以角速度ω顺时针匀速转动至另一端落在导轨B上.如两导轨间是一磁感应强度为B,方向垂直于纸面向里的匀强磁场、不计一切电阻,则在上述整个转动过程中( )| A. | 金属杆两端的电压不断增大 | B. | O′端的电势总是高于O端的电势 | ||
| C. | 两导轨间的最大电压是Bl2ω | D. | 两导轨间的平均电压是$\frac{3\sqrt{3}B{l}^{2}ω}{2π}$ |
| A. | 密度减小 | B. | 密度不变 | C. | 压强增大 | D. | 压强不变 |
| A. | 验证力的平行四边形定则 | |
| B. | 探究加速度与物体质量、物体受力的关系 | |
| C. | 探究匀变速直线运动的规律 | |
| D. | 探究弹簧的弹力和弹簧伸长的关系 |
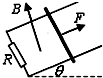 如图所示,下端接有电阻R的“U”形光滑金属导轨与水平面成θ角,导轨所在空间有一与导轨平面垂直的匀强磁场.导轨上有一个金属棒,金属棒与两导轨垂直且接触良好,在沿着斜面向上且与棒垂直的拉力F作用下,金属棒沿导轨匀速上滑,则下列说法正确的是( )
如图所示,下端接有电阻R的“U”形光滑金属导轨与水平面成θ角,导轨所在空间有一与导轨平面垂直的匀强磁场.导轨上有一个金属棒,金属棒与两导轨垂直且接触良好,在沿着斜面向上且与棒垂直的拉力F作用下,金属棒沿导轨匀速上滑,则下列说法正确的是( )| A. | 拉力做的功等于该金属棒的机械能的增量 | |
| B. | 拉力做的功等于该金属棒重力势能的增量与回路产生的热量之和 | |
| C. | 该金属棒所受的拉力、安培力、重力做功之和等于回路产生的热量 | |
| D. | 安培力对该金属棒做的功的大小等于回路中产生的电能 |
| A. | 滑动摩擦力一定对物体做负功,静摩擦力一定对物体不做功 | |
| B. | 一对作用力与反作用力对物体做功的代数和一定为零 | |
| C. | 某力对物体做负功,可以说成“物体克服某力做功” | |
| D. | 一个受变力作用的物体做曲线运动时,其合力的瞬时功率不可能为零 |