题目内容
10. 空间有一圆柱形匀强磁场区域,该区域的横截面的半径为R,磁场方向垂直横截面.一质量为m、电荷量为q(q>0)的粒子以速率v0沿横截面的某直径射入磁场,离开磁场时速度方向偏离入射方向60°.不计重力,该磁场的磁感应强度大小为( )
空间有一圆柱形匀强磁场区域,该区域的横截面的半径为R,磁场方向垂直横截面.一质量为m、电荷量为q(q>0)的粒子以速率v0沿横截面的某直径射入磁场,离开磁场时速度方向偏离入射方向60°.不计重力,该磁场的磁感应强度大小为( )| A. | $\frac{\sqrt{3}m{v}_{0}}{3qR}$ | B. | $\frac{m{v}_{0}}{qR}$ | C. | $\frac{\sqrt{3}m{v}_{0}}{qR}$ | D. | $\frac{3m{v}_{0}}{qR}$ |
分析 带正电的粒子垂直磁场方向进入圆形匀强磁场区域,由洛伦兹力提供向心力,由几何知识求出轨迹半径r,根据牛顿第二定律求出磁场的磁感应强度.
解答 解:带正电的粒子垂直磁场方向进入圆形匀强磁场区域,由洛伦兹力提供向心力而做匀速圆周运动,画出轨迹如图,根据几何知识得知,
轨迹的圆心角等于速度的偏向角60°,
且轨迹的半径为 r=Rcot30°=$\sqrt{3}$R,
由牛顿第二定律得:qv0B=m$\frac{{v}_{0}^{2}}{r}$,
解得:$B=\frac{\sqrt{3}m{v}_{0}}{3qR}$;
故选:A.
点评 本题是带电粒子在匀强磁场中运动的问题,画轨迹是关键,是几何知识和动力学知识的综合应用,常规问题.

练习册系列答案
相关题目
20.下列关于质点的说法中正确的是( )
| A. | 只要是体积很小的球体就可以视为质点 | |
| B. | 研究一汽车从长治到太原的运动路线时可以将其视为质点 | |
| C. | 因为太阳的体积太大了,所以任何情况下都不可以将其视为质点 | |
| D. | 观察月相时可以将月亮视为质点 |
1. 在空间直角坐标系O-xyz中,有一四面体C-AOB,C、A、O、B为四面体的四个顶点,且O(0,0,0)、A(L,0,0)、B(0,L,0)、C(0,0,L),D(2L,0,0)是x轴上一点,在坐标原点O处固定着+Q的点电荷,下列说法正确的是( )
在空间直角坐标系O-xyz中,有一四面体C-AOB,C、A、O、B为四面体的四个顶点,且O(0,0,0)、A(L,0,0)、B(0,L,0)、C(0,0,L),D(2L,0,0)是x轴上一点,在坐标原点O处固定着+Q的点电荷,下列说法正确的是( )
 在空间直角坐标系O-xyz中,有一四面体C-AOB,C、A、O、B为四面体的四个顶点,且O(0,0,0)、A(L,0,0)、B(0,L,0)、C(0,0,L),D(2L,0,0)是x轴上一点,在坐标原点O处固定着+Q的点电荷,下列说法正确的是( )
在空间直角坐标系O-xyz中,有一四面体C-AOB,C、A、O、B为四面体的四个顶点,且O(0,0,0)、A(L,0,0)、B(0,L,0)、C(0,0,L),D(2L,0,0)是x轴上一点,在坐标原点O处固定着+Q的点电荷,下列说法正确的是( )| A. | A、B、C三点的电场强度相同 | |
| B. | 电势差UOA=UAD | |
| C. | 将一电子由C点分别移动到A、B两点,电场力做功相等 | |
| D. | 电子在A点的电势能小于在D点的电势能 |
5. 设有一冰球以匀速v0沿直线运动在光滑无摩擦的水平平面上从a点运动到b点,忽略空气阻力.图为俯视图.当冰球运动到b点时受到图示中黑箭头方向的快速一击.这之后冰球有可能沿如下哪一条轨迹运动?( )
设有一冰球以匀速v0沿直线运动在光滑无摩擦的水平平面上从a点运动到b点,忽略空气阻力.图为俯视图.当冰球运动到b点时受到图示中黑箭头方向的快速一击.这之后冰球有可能沿如下哪一条轨迹运动?( )
 设有一冰球以匀速v0沿直线运动在光滑无摩擦的水平平面上从a点运动到b点,忽略空气阻力.图为俯视图.当冰球运动到b点时受到图示中黑箭头方向的快速一击.这之后冰球有可能沿如下哪一条轨迹运动?( )
设有一冰球以匀速v0沿直线运动在光滑无摩擦的水平平面上从a点运动到b点,忽略空气阻力.图为俯视图.当冰球运动到b点时受到图示中黑箭头方向的快速一击.这之后冰球有可能沿如下哪一条轨迹运动?( )| A. |  | B. |  | C. |  | D. |  |
2. 如图所示,电子在电势差为U1的加速电场中由静止开始运动,然后射入电势差为U2的两块平行板间的电场中,入射方向跟极板平行.整个装置处在真空中,重力可忽略.在满足电子能射出平行板区的条件下,下述四种情况中,一定能使电子的偏转角θ变大的是( )
如图所示,电子在电势差为U1的加速电场中由静止开始运动,然后射入电势差为U2的两块平行板间的电场中,入射方向跟极板平行.整个装置处在真空中,重力可忽略.在满足电子能射出平行板区的条件下,下述四种情况中,一定能使电子的偏转角θ变大的是( )
 如图所示,电子在电势差为U1的加速电场中由静止开始运动,然后射入电势差为U2的两块平行板间的电场中,入射方向跟极板平行.整个装置处在真空中,重力可忽略.在满足电子能射出平行板区的条件下,下述四种情况中,一定能使电子的偏转角θ变大的是( )
如图所示,电子在电势差为U1的加速电场中由静止开始运动,然后射入电势差为U2的两块平行板间的电场中,入射方向跟极板平行.整个装置处在真空中,重力可忽略.在满足电子能射出平行板区的条件下,下述四种情况中,一定能使电子的偏转角θ变大的是( )| A. | U1变小、U2变大 | B. | U1变大、U2变大 | C. | U1变大、U2变小 | D. | U1变小、U2不变 |
19. 如图为两个点电荷在真空中所产生电场的电场线(方向未标出).图中C点为两点电荷连线的中点,MN为两点电荷连线的中垂线,D为中垂线上的一点,电场线的分布关于MN左右对称.则下列说法中正确的是( )
如图为两个点电荷在真空中所产生电场的电场线(方向未标出).图中C点为两点电荷连线的中点,MN为两点电荷连线的中垂线,D为中垂线上的一点,电场线的分布关于MN左右对称.则下列说法中正确的是( )
 如图为两个点电荷在真空中所产生电场的电场线(方向未标出).图中C点为两点电荷连线的中点,MN为两点电荷连线的中垂线,D为中垂线上的一点,电场线的分布关于MN左右对称.则下列说法中正确的是( )
如图为两个点电荷在真空中所产生电场的电场线(方向未标出).图中C点为两点电荷连线的中点,MN为两点电荷连线的中垂线,D为中垂线上的一点,电场线的分布关于MN左右对称.则下列说法中正确的是( )| A. | 这两点电荷一定是等量异种电荷 | B. | 这两点电荷一定是等量同种电荷 | ||
| C. | D、C两点的电场强度一定相等 | D. | C点的电场强度比D点的电场强度小 |
20. 如图,一同学分别在同一直线上的ABC三个位置投掷篮球,结果都垂直击中篮框,速度分别为vA、vB、vC,若篮球出手时高度相同,出手速度与水平方向夹角分别是θA、θB、θC,下列说法正确的是( )
如图,一同学分别在同一直线上的ABC三个位置投掷篮球,结果都垂直击中篮框,速度分别为vA、vB、vC,若篮球出手时高度相同,出手速度与水平方向夹角分别是θA、θB、θC,下列说法正确的是( )
 如图,一同学分别在同一直线上的ABC三个位置投掷篮球,结果都垂直击中篮框,速度分别为vA、vB、vC,若篮球出手时高度相同,出手速度与水平方向夹角分别是θA、θB、θC,下列说法正确的是( )
如图,一同学分别在同一直线上的ABC三个位置投掷篮球,结果都垂直击中篮框,速度分别为vA、vB、vC,若篮球出手时高度相同,出手速度与水平方向夹角分别是θA、θB、θC,下列说法正确的是( )| A. | vA>vB>vC | B. | vA=vB=vC | C. | θA=θB=θC | D. | θA>θB>θC |

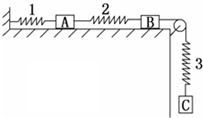 如图所示,质量不等的三个物块A、B、C用劲度系数完全相同的三个弹簧1、2、3依次连接着处于静止状态,A、B在水平桌面上,C绕过定滑轮悬挂在桌面外,此时弹簧1、2、3的伸长量分别为0、2cm、3cm,已知C的质量为mc=3kg,(取g=10m/s2)则
如图所示,质量不等的三个物块A、B、C用劲度系数完全相同的三个弹簧1、2、3依次连接着处于静止状态,A、B在水平桌面上,C绕过定滑轮悬挂在桌面外,此时弹簧1、2、3的伸长量分别为0、2cm、3cm,已知C的质量为mc=3kg,(取g=10m/s2)则