题目内容
5. 如图所示,I和II是人造卫星绕地球运动的两条圆轨道,轨道半径rI<rII.设两卫星A、B绕地球做匀速圆周运动的周期分别为TA、TB,且TA>TB.关于两卫星可能的运行轨道,下列判断正确的是( )
如图所示,I和II是人造卫星绕地球运动的两条圆轨道,轨道半径rI<rII.设两卫星A、B绕地球做匀速圆周运动的周期分别为TA、TB,且TA>TB.关于两卫星可能的运行轨道,下列判断正确的是( )| A. | A卫星位于轨道I上、B卫星位于轨道II上 | |
| B. | A卫星位于轨道II上、B卫星位于轨道I上 | |
| C. | A、B两卫星都位于轨道I上 | |
| D. | A、B两卫星都位于轨道II上 |
分析 卫星绕地球做匀速圆周运动,由万有引力提供卫星圆周运动的向心力,据此分析描述圆周运动物理量与半径的关系即可.
解答 解:卫星绕地球做匀速圆周运动,由万有引力提供向心力,则有:
G$\frac{Mm}{{r}_{\;}^{2}}$=m$\frac{4{π}_{\;}^{2}}{{T}_{\;}^{2}}$r=ma,所以得,卫星的周期 T=2π$\sqrt{\frac{{r}_{\;}^{3}}{GM}}$,
由题:${T}_{A}^{\;}>{T}_{B}^{\;}$,由T=2π$\sqrt{\frac{{r}_{\;}^{3}}{GM}}$,知A的轨道半径大于B的轨道半径,即${r}_{A}^{\;}>{r}_{B}^{\;}$,I和II是人造卫星绕地球运动的两条圆轨道,轨道半径${r}_{Ⅰ}^{\;}<{r}_{Ⅱ}^{\;}$,所以A卫星位于轨道Ⅱ上,B卫星位于轨道Ⅰ上,故B正确,ACD错误;
故选:B
点评 知道卫星问题的基本思路:万有引力提供圆周运动向心力,掌握万有引力和向心力的表达式是正确解题的关键.

练习册系列答案
相关题目
13.如图所示,a、b是在地球大气层外圆形轨道上运行的两颗人造卫星,下列说法中正确的是( )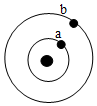

| A. | 卫星6的线速度大于卫星a的线速度 | |
| B. | 卫星b的向心加速度小于卫星a的向心加速度 | |
| C. | 卫星a的运行周期大于卫星b的运行周期 | |
| D. | 卫星a的角速度小于卫星b的角速度 |
20. 如图所示,飞机起飞时以300km/h的速度斜向上飞,飞行的方向与水平面的夹角为37°(sin37°=0.6,cos37°=0.8),则飞行的( )
如图所示,飞机起飞时以300km/h的速度斜向上飞,飞行的方向与水平面的夹角为37°(sin37°=0.6,cos37°=0.8),则飞行的( )
 如图所示,飞机起飞时以300km/h的速度斜向上飞,飞行的方向与水平面的夹角为37°(sin37°=0.6,cos37°=0.8),则飞行的( )
如图所示,飞机起飞时以300km/h的速度斜向上飞,飞行的方向与水平面的夹角为37°(sin37°=0.6,cos37°=0.8),则飞行的( )| A. | 水平分速度为180km/h | B. | 水平分速度为240km/h | ||
| C. | 竖直分速度为180km/h | D. | 竖直分速度为240km/h |
17.做平抛运动的物体在空中运动的时间( )
| A. | 仅由下落的高度决定 | |
| B. | 仅由抛出时的速度决定 | |
| C. | 由下落的高度和抛出时的速度共同决定 | |
| D. | 与下落的高度和抛出时的速度都无关 |
14.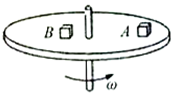 如图所示,两个完全相同的物块A、B置于绕竖直轴匀速转动的水平圆盘上,A与转轴间的距离是B与转轴间距离的2倍,两物块均相对于圆盘静止,下列说法正确的是( )
如图所示,两个完全相同的物块A、B置于绕竖直轴匀速转动的水平圆盘上,A与转轴间的距离是B与转轴间距离的2倍,两物块均相对于圆盘静止,下列说法正确的是( )
 如图所示,两个完全相同的物块A、B置于绕竖直轴匀速转动的水平圆盘上,A与转轴间的距离是B与转轴间距离的2倍,两物块均相对于圆盘静止,下列说法正确的是( )
如图所示,两个完全相同的物块A、B置于绕竖直轴匀速转动的水平圆盘上,A与转轴间的距离是B与转轴间距离的2倍,两物块均相对于圆盘静止,下列说法正确的是( )| A. | 两物块的角速度相同 | B. | 两物块的线速度相同 | ||
| C. | B物块的角速度大 | D. | B物块的线速度大 |
6.下列运动,机械能守恒的是( )
| A. | 小球做自由落体运动 | B. | 汽车刹车时的运动 | ||
| C. | 物体沿光滑斜面自由下滑 | D. | 雨滴匀速下落 |
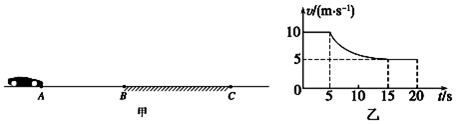




 如图所示,一个质量为10kg的物体放在光滑水平地面上,用50N的水平拉力F使物体由静止开始做匀加速直线运动.求:
如图所示,一个质量为10kg的物体放在光滑水平地面上,用50N的水平拉力F使物体由静止开始做匀加速直线运动.求: