题目内容
4.我国发射的北斗系列卫星的轨道位于赤道上方,轨道半径为r,绕行方向与地球自转方向相同.设地球自转角速度为ω0,地球半径为R,地球表面重力加速度为g.设某一时刻,卫星通过赤道上某建筑物的上方,则当它再一次通过该建筑物上方时,所经历的时间为( )| A. | $\frac{2π}{{\sqrt{\frac{{g{R^2}}}{r^3}}-{ω_0}_{\;}}}$ | B. | 2π($\sqrt{\frac{{r}^{3}}{g{R}^{2}}}$+$\frac{1}{{ω}_{0}}$) | C. | 2π$\sqrt{\frac{{r}^{3}}{g{R}^{2}}}$ | D. | 2π$\sqrt{\frac{g{R}^{2}}{{r}^{3}}}$+ω0 |
分析 根据人造卫星的万有引力等于向心力,列式求出角速度的表达式,卫星再次经过某建筑物的上空,地球多转动一圈.
解答 解:人造卫星绕地球做匀速圆周运动,根据万有引力提供向心力,设卫星的质量为m、轨道半径为r、地球质量为M,有
F=F向
F=G$\frac{Mm}{{r}^{2}}$
F向=mω2r
因而
G$\frac{Mm}{{r}^{2}}$=mω2r
解得
ω=$\sqrt{\frac{GM}{{r}^{3}}}$ ①
卫星再次经过某建筑物的上空,卫星多转动一圈,有
(ω-ω0)t=2π ②
地球表面的重力加速度为
g=$\frac{GM}{{R}^{2}}$ ③
联立①②③后,解得
t=$\frac{2π}{{\sqrt{\frac{{g{R^2}}}{r^3}}-{ω_0}_{\;}}}$.
故选:A.
点评 本题关键:(1)根据万有引力提供向心力求解出角速度;(2)根据地球表面重力等于万有引力得到重力加速度表达式;(3)根据多转动一圈后再次到达某建筑物上空列式.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
14.宇航员在地球和某星球表面做了两个对比实验.实验一:在该星球和地球上以同样的高度和初速度平抛同一物体,发现其水平射程是地球上的4倍.实验二:飞船绕该星球表面的运行周期是它绕地球表面运行周期的2倍.则该星球与地球的质量之比和半径之比分别是( )
| A. | $\frac{1}{256}$,$\frac{1}{4}$ | B. | $\frac{1}{256}$,$\frac{1}{8}$ | C. | $\frac{1}{64}$,$\frac{1}{4}$ | D. | $\frac{1}{16}$,$\frac{1}{1}$ |
9.下列叙述正确的是( )
| A. | 理想气体压强越大,分子的平均动能越大 | |
| B. | 自然界中进行的涉及热现象的宏观过程都具有方向性 | |
| C. | 外界对理想气体做正功,气体的内能不一定增大 | |
| D. | 温度升高,物体内每个分子的热运动速率都增大 |
1.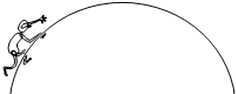 某屋顶为半球形,一人在半球形屋顶上向上缓慢爬行(如图所示),他在向上爬的过程中( )
某屋顶为半球形,一人在半球形屋顶上向上缓慢爬行(如图所示),他在向上爬的过程中( )
 某屋顶为半球形,一人在半球形屋顶上向上缓慢爬行(如图所示),他在向上爬的过程中( )
某屋顶为半球形,一人在半球形屋顶上向上缓慢爬行(如图所示),他在向上爬的过程中( )| A. | 屋顶对他的支持力不变 | B. | 屋顶对他的支持力变大 | ||
| C. | 屋顶对他的摩擦力不变 | D. | 屋顶对他的摩擦力变小 |
 封闭在气缸内一定质量的理想气体由状态A变到状态D,其体积V与热力学温度T关系如图所示,该气体的摩尔质量为M,状态A的体积为V0,温度为T0,O、A、D三点在同一直线上,阿伏伽德罗常数为NA.
封闭在气缸内一定质量的理想气体由状态A变到状态D,其体积V与热力学温度T关系如图所示,该气体的摩尔质量为M,状态A的体积为V0,温度为T0,O、A、D三点在同一直线上,阿伏伽德罗常数为NA.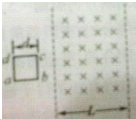 如图所示,正方形线框abcd的边长为d,向右通过宽为L的匀强磁场,且d<1,则在线框进入过程中穿过线圈的磁通量变化情况是增大,感应电流的磁场对磁通量变化起阻碍作用,线框中感应电流方向是abcda;在线框移出磁场的过程中穿过线圈的磁感应量变化情况是减小,感应电流的磁场对磁通量变化起阻碍作用,线框中感应电流方向是adcba.
如图所示,正方形线框abcd的边长为d,向右通过宽为L的匀强磁场,且d<1,则在线框进入过程中穿过线圈的磁通量变化情况是增大,感应电流的磁场对磁通量变化起阻碍作用,线框中感应电流方向是abcda;在线框移出磁场的过程中穿过线圈的磁感应量变化情况是减小,感应电流的磁场对磁通量变化起阻碍作用,线框中感应电流方向是adcba.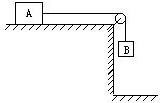 如图所示,mA=4kg,mB=1kg,A与桌面间的动摩擦因数μ=0.2,B与地面间的距离s=0.8m,A、B间绳子足够长,A、B原来静止,求:
如图所示,mA=4kg,mB=1kg,A与桌面间的动摩擦因数μ=0.2,B与地面间的距离s=0.8m,A、B间绳子足够长,A、B原来静止,求: