题目内容
宇航员站在一星球表面上的某高处,沿水平方向抛出一个小球,经过时间t小球落到星球表面,测得抛出点与落地点之间的距离为L,若抛出时的初速度增大到原来的2倍,则抛出点与落地点间的距离为 .已知两落地点在同一水平面上,该星球的半径为R,万有引力常量为G,试求该星球的质量M.
.已知两落地点在同一水平面上,该星球的半径为R,万有引力常量为G,试求该星球的质量M.
答案:略
解析:
解析:
|
星球的质量 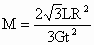 . .
设抛出点的高度为 h,第一次平抛射程为x,小球的质量为m,该星球表面的重力加速度为g,则由几何关系有: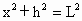 ① ①
由平抛运动规律得,在平抛初速度增大到 2倍时,其水平射程也增大到2倍,即2x,即有: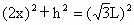 . ② . ②
又因小球在竖直方向上自由下落: 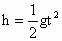 ③ ③
由万有引力定律和牛顿第二定律得: 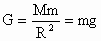 ④ ④
综合以上四式可得 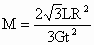 . .
此题综合运用了万有引力定律、牛顿第二定律以及平抛运动的规律,把在地球表面上的平抛运动的情景迁移到该星球上,解题的关键是要挖掘上题中的隐藏条件,即小球受到的重力近似等于星球对它的万有引力. |

练习册系列答案
相关题目