题目内容
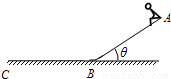如图为一滑梯的示意图，滑梯的长度AB为L=5.0m，倾角θ=37°．BC段为与滑梯平滑连接的水平地面．一个小孩从滑梯顶端A由静止开始滑下，离开B点后在地面上滑行了s=2.25m后停下．小孩与滑梯间的动摩擦因数为μ=0.3．不计空气阻力．取g=10m/s2．已知sin 37°=0.6，cos 37°=0.8．求：（1）小孩沿滑梯下滑时的加速度a的大小；
（2）小孩滑到滑梯底端B时的速度v的大小；
（3）小孩与地面间的动摩擦因数μ′．
【答案】分析：（1）小孩下滑过程中受到重力、滑梯的支持力和滑动摩擦力，根据牛顿第二定律求出加速度．
（2）小孩做匀加速直线运动，由速度位移关系公式小孩滑到滑梯底端B时的速度v的大小．
（3）小孩在地面上滑行时，水平方向受到滑动摩擦力，做匀减速运动，知道位移、末速度和初速度，先由速度位移关系式求出加速度，再由牛顿第二定律求出动摩擦因数μ′．
解答：
解：（1）小孩受力如图所示
由牛顿运动定律，得mgsin θ-μFN=ma，
FN-mgcosθ=0
解得a=g（sin θ-μcos θ）=3.6 m/s2
（2）由v2=2aL，得到v=6 m/s
（3）小孩在水平面上滑行时，
由匀变速直线运动，得0-v2=2a′s
又由牛顿第二定律得μ′mg=ma′
代入解得μ′=0.8
答：（1）小孩沿滑梯下滑时的加速度a的大小为3.6m/s2；
（2）小孩滑到滑梯底端B时的速度v的大小为6m/s；
（3）小孩与地面间的动摩擦因数μ′=0.8．
点评：牛顿定律常常用来解决动力学两类问题，一类是已知受到受力情况确定运动情况，另一类是根据运动情况研究受力情况．加速度是联系力和运动的桥梁，是必求的量．
（2）小孩做匀加速直线运动，由速度位移关系公式小孩滑到滑梯底端B时的速度v的大小．
（3）小孩在地面上滑行时，水平方向受到滑动摩擦力，做匀减速运动，知道位移、末速度和初速度，先由速度位移关系式求出加速度，再由牛顿第二定律求出动摩擦因数μ′．
解答：
解：（1）小孩受力如图所示由牛顿运动定律，得mgsin θ-μFN=ma，
FN-mgcosθ=0
解得a=g（sin θ-μcos θ）=3.6 m/s2
（2）由v2=2aL，得到v=6 m/s
（3）小孩在水平面上滑行时，
由匀变速直线运动，得0-v2=2a′s
又由牛顿第二定律得μ′mg=ma′
代入解得μ′=0.8
答：（1）小孩沿滑梯下滑时的加速度a的大小为3.6m/s2；
（2）小孩滑到滑梯底端B时的速度v的大小为6m/s；
（3）小孩与地面间的动摩擦因数μ′=0.8．
点评：牛顿定律常常用来解决动力学两类问题，一类是已知受到受力情况确定运动情况，另一类是根据运动情况研究受力情况．加速度是联系力和运动的桥梁，是必求的量．
练习册系列答案
全优点练单元计划系列答案
相关题目
（2011?通州区模拟）如图为一滑梯的示意图，滑梯的长度AB为L=5.0m，倾角θ=37°．BC段为与滑梯平滑连接的水平地面．一个小孩从滑梯顶端A由静止开始滑下，离开B点后在地面上滑行了s=2.25m后停下．小孩与滑梯间的动摩擦因数为μ=0.3．不计空气阻力．取g=10m/s2．已知sin 37°=0.6，cos 37°=0.8．求：
如图为一滑梯的示意图，滑梯的长度AB为 L=5.0m，倾角θ=37°，BC段为与滑梯平滑连接的水平地面．一个小孩从滑梯顶端由静止开始滑下．小孩与滑梯间的动摩擦因数为μ=0.3，与水平地面间的动摩擦因数为μ′=0.5．不计空气阻力．取g=10m/s2．已知sin37°=0.6，cos37°=0.8．求：
=37°。BC段为与滑梯平滑连接的水平地面。一个小孩从滑梯顶端由静止开始下滑，离开B点后在地面上滑行了L=2.25m后停下，小孩与滑
梯间的动摩擦因数为
=0.3.不计空气阻力。取g=10m/s2，已知sin37°=0.6,cos37°=0.8。求：
的大小；（7分）
