题目内容
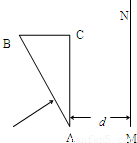 如图所示,有一截面是直角三角形的棱镜ABC,∠A=30°.它对红光的折射率为n1.对紫光的折射率为n2.在距AC边d处有一与AC平行的光屏,现有由以上两种色光组成的很细的光束垂直AB边射入棱镜.
如图所示,有一截面是直角三角形的棱镜ABC,∠A=30°.它对红光的折射率为n1.对紫光的折射率为n2.在距AC边d处有一与AC平行的光屏,现有由以上两种色光组成的很细的光束垂直AB边射入棱镜.①红光和紫光在棱镜中的传播速度比为多少?
②若两种光都能从AC面射出,求在光屏MN上两光点间的距离.
【答案】分析:①根据v=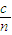 求出红光和紫光在棱镜中的传播速度比.
求出红光和紫光在棱镜中的传播速度比.
②两种色光组成的很细的光束垂直AB边射入棱镜,在AB面上不发生偏折,到达AC面上,根据几何关系求出入射角的大小,根据折射定律求出折射角,再根据几何关系求出光屏MN上两光点间的距离
解答: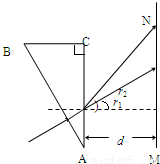 解:根据v=
解:根据v=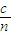 得:
得:
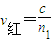 ,
,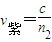
所以有: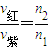
②根据几何关系,光从AC面上折射时的入射角为30°,
根据折射定律有:
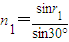
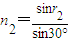
则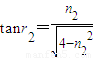 ,tan
,tan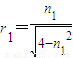
所以x=d(tanr2-tanr1)=d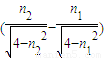 .
.
答:①红光和紫光在棱镜中的传播速度比为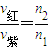 .
.
②光屏MN上两光点间的距离为d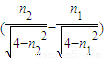 .
.
点评:解决本题的关键掌握v=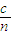 和折射定律n=
和折射定律n=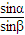 ,以及能够熟练地运用数学几何关系.
,以及能够熟练地运用数学几何关系.
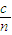 求出红光和紫光在棱镜中的传播速度比.
求出红光和紫光在棱镜中的传播速度比.②两种色光组成的很细的光束垂直AB边射入棱镜,在AB面上不发生偏折,到达AC面上,根据几何关系求出入射角的大小,根据折射定律求出折射角,再根据几何关系求出光屏MN上两光点间的距离
解答:
 解:根据v=
解:根据v=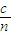 得:
得: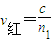 ,
,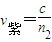
所以有:
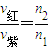
②根据几何关系,光从AC面上折射时的入射角为30°,
根据折射定律有:
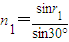
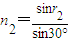
则
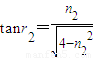 ,tan
,tan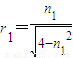
所以x=d(tanr2-tanr1)=d
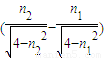 .
.答:①红光和紫光在棱镜中的传播速度比为
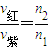 .
.②光屏MN上两光点间的距离为d
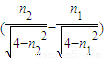 .
.点评:解决本题的关键掌握v=
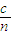 和折射定律n=
和折射定律n=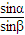 ,以及能够熟练地运用数学几何关系.
,以及能够熟练地运用数学几何关系. 
练习册系列答案
 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目
 如图所示,有一截面是直角三角形的棱镜ABC,∠A=30°.它对红光的折射率为n1.对紫光的折射率为n2.在距AC边d处有一与AC平行的光屏,现有由以上两种色光组成的很细的光束垂直AB边射入棱镜.
如图所示,有一截面是直角三角形的棱镜ABC,∠A=30°.它对红光的折射率为n1.对紫光的折射率为n2.在距AC边d处有一与AC平行的光屏,现有由以上两种色光组成的很细的光束垂直AB边射入棱镜. 如图所示,有一截面是直角三角形的棱镜ABC,∠A=30°.它对红光的折射率为n1,对紫光的折射率为n2.现有由以上两种色光组成的很细的光束垂直AB边射入棱镜.
如图所示,有一截面是直角三角形的棱镜ABC,∠A=30°.它对红光的折射率为n1,对紫光的折射率为n2.现有由以上两种色光组成的很细的光束垂直AB边射入棱镜. (2011?娄底模拟)如图所示,有一截面是直角三角形的棱镜ABC,∠A=30°.它对红光的折射率为n1.对紫光的折射率为n2.在距AC边为d处有一与AC平行的光屏.现有由以上两种色光组成的很细的光束垂直AB边射入棱镜.
(2011?娄底模拟)如图所示,有一截面是直角三角形的棱镜ABC,∠A=30°.它对红光的折射率为n1.对紫光的折射率为n2.在距AC边为d处有一与AC平行的光屏.现有由以上两种色光组成的很细的光束垂直AB边射入棱镜. (1)下列说法中正确的是
(1)下列说法中正确的是 物理一一选修3-4:
物理一一选修3-4: