题目内容
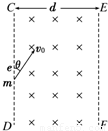 匀强磁场的磁感应强度为B,宽度为d,边界为CD和EF.一电子从CD边界外侧以速率v垂直射入匀强磁场,入射方向与CD边界间夹角为θ.已知电子的质量为m,电荷量为e,为使电子能从磁场的另一侧EF射出,求电子的速率v至少多大?若θ角可取任意值,半径的最小值是多少?
匀强磁场的磁感应强度为B,宽度为d,边界为CD和EF.一电子从CD边界外侧以速率v垂直射入匀强磁场,入射方向与CD边界间夹角为θ.已知电子的质量为m,电荷量为e,为使电子能从磁场的另一侧EF射出,求电子的速率v至少多大?若θ角可取任意值,半径的最小值是多少?
【答案】分析:粒子在磁场中做匀速圆周运动,当其轨迹恰好与EF边相切时,轨迹半径最小,对应的速度最小.由几何知识求出,再牛顿定律求出速度的范围.运用数学知识,由θ的取值来确定速度的最小,从而求出半径的最小值.
解答: 解:如图所示.电子恰好从EF边射出时,由几何知识可得:
解:如图所示.电子恰好从EF边射出时,由几何知识可得:
r+rcosθ=d…①
由牛顿第二定律: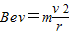
得:r=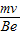 …②
…②
由①②得:v= …③
…③
故电子要射出磁场,速率至少应为
由③式可知,θ=0°时,v= 最小,
最小,
由②式知此时半径最小,rmin=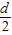 ,
,
也可由轨迹分析得出上述结论.
答:为使电子能从磁场的另一侧EF射出,求电子的速率v至少为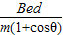 ;若θ角可取任意值,v的最小值是
;若θ角可取任意值,v的最小值是 .
.
点评:本题考查圆周运动的边界问题的求解方法.当入射速率v很小时,电子会在磁场中转动一段圆弧后又从CD一侧射出,速率越大,轨道半径越大,当轨道与边界EF相切时,电子恰好不能从EF射出,
解答:
 解:如图所示.电子恰好从EF边射出时,由几何知识可得:
解:如图所示.电子恰好从EF边射出时,由几何知识可得:r+rcosθ=d…①
由牛顿第二定律:
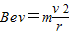
得:r=
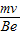 …②
…②由①②得:v=
 …③
…③故电子要射出磁场,速率至少应为

由③式可知,θ=0°时,v=
 最小,
最小,由②式知此时半径最小,rmin=
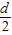 ,
,也可由轨迹分析得出上述结论.
答:为使电子能从磁场的另一侧EF射出,求电子的速率v至少为
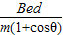 ;若θ角可取任意值,v的最小值是
;若θ角可取任意值,v的最小值是 .
.点评:本题考查圆周运动的边界问题的求解方法.当入射速率v很小时,电子会在磁场中转动一段圆弧后又从CD一侧射出,速率越大,轨道半径越大,当轨道与边界EF相切时,电子恰好不能从EF射出,

练习册系列答案
相关题目
 如图所示,将一根质量为M=0.06kg的均匀导线杆弯成矩形闭合导线框abcd,其ab=cd=L1=0.1m,bc=ad=L2=0.2m.它的ad边由aO、dO′两轴承支撑沿水平放置,导线框位于竖直平面内,bc段中点固定一质量为m=0.02kg的小金属球,整个装置处在一方向竖直向上的匀强磁场中.当导线框中通以大小恒为1A的恒定电流I时,整个装置以OO′为轴从静止开始逆时针转动.
如图所示,将一根质量为M=0.06kg的均匀导线杆弯成矩形闭合导线框abcd,其ab=cd=L1=0.1m,bc=ad=L2=0.2m.它的ad边由aO、dO′两轴承支撑沿水平放置,导线框位于竖直平面内,bc段中点固定一质量为m=0.02kg的小金属球,整个装置处在一方向竖直向上的匀强磁场中.当导线框中通以大小恒为1A的恒定电流I时,整个装置以OO′为轴从静止开始逆时针转动. 如图所示,一质量m=0.1kg的金属棒ab可沿接有电阻R=1Ω的足够长的竖直导体框架无摩擦地滑动,框架间距L=50cm,匀强磁场的磁感应强度B=0.4T,方向如图示,其余电阻均不计.若棒ab由静止开始沿框架下落,且与框保持良好接触,那么在下落的前一阶段,棒ab将做
如图所示,一质量m=0.1kg的金属棒ab可沿接有电阻R=1Ω的足够长的竖直导体框架无摩擦地滑动,框架间距L=50cm,匀强磁场的磁感应强度B=0.4T,方向如图示,其余电阻均不计.若棒ab由静止开始沿框架下落,且与框保持良好接触,那么在下落的前一阶段,棒ab将做

