题目内容
总质量为M的列车，沿水平轨道匀速地前进，其末节车厢质量为m，中途某时刻脱节，脱节后的列车仍以原来的牵引力继续前进。从脱节开始到司机发觉，列车已从脱节位置向前行驶L的距离。司机立即关闭油门，撤去牵引力。设运动时阻力与车重成正比。当脱节车厢和列车这两部分都停止运动时，它们的距离是多少？
【答案】
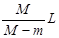
【解析】脱钩前匀速运动，所以牵引力和总的阻力相等．设速度为V1.
脱钩后对列车：牵引力没变，阻力减少了kmg，所以合力为kmg．所以有
kmg=(M-m)a
在他发现脱钩时列车的速度为V2,有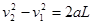
从脱钩开始到车厢停下来需要的车厢运动的距离S1=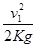
从脱钩到列车停下来列车运动的距离S2=L+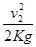
所以差△S=S2-S1=ML/(M-m)
练习册系列答案
相关题目
