Question

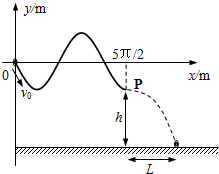如图所示，将一个光滑金属杆弯成y=-2sinx（0≤x≤

5π

2

）（单位：m）的形状，一个小环从x=0处以沿着杆的初速v₀出发，最终从x=

5π

2

处的P点水平抛出，下落高度h=1.8m后掉落在地面上．试求
（1）v₀满足什么条件时小环才能从P点水平抛出？
（2）小环从P点水平抛出的射程L和v₀的函数关系式是怎样的？

Answer 1

分析：（1）因为小环必须越过最高点后才能抛出，根据动能定理即可求得最小初速度；
（2）小环才能从P点水平抛出做平抛运动，根据平抛运动的规律就可以得出P点速度和L的关系，从起点到抛出点运用动能定理就可以得出环从P点水平抛出的射程L和v₀的函数关系式．

解答：解：（1）因为小环必须越过最高点后才能抛出，根据动能定理得：
          -mgA=0-

1

2

m

v

2 0

          而根据题意可知：A=2m
         解得：v₀=

40

m/s
  所以当v₀≥

40

m/s时才能从P点水平抛出．
（2）设平抛出的速度v₁，从起点到抛出点列动能定理mgA=

1

2

m

v

2 1

-

1

2

m

v

2 0

，A=2m
         得v₁=

40+ v 2 0

     抛出后做平抛运动，根据平抛运动的规律可得：
             h=

1

2

gt2，L=v₁t
         所以：L=

2h g

?v1=

3

5

40+ v 2 0

       当初速度v₀≥

40

m/s时才能从P点抛出，关系式为：L=

3

5

40+ v 2 0

；
       当初速度v₀＜

40

m/s时，不能从P点抛出，L=0．
答：（1）当初速度v₀≥

40

m/s时才能从P点抛出；（2）当初速度v₀≥

40

m/s时才能从P点抛出，关系式为：L=

3

5

40+ v 0 2

；当初速度v₀＜

40

m/s时，不能从P点抛出，L=0．

点评：该题是物理模型和数学知识相结合的问题，要明确小环的运动过程，选取适当的过程运用动能定理解题，难度适中．