题目内容
如图是齿轮传动装置，两个齿轮的半径比ra：rb为1：2，a、b为两轮子边缘点，c 为大轮半径的中点，当齿轮转动时，υa：υb：υc= ，
ωa：ωb：ωc= ．
【答案】分析：根据两齿轮边缘上各点的线速度大小相等和同一齿轮上各点的角速度相同，由公式v=ωr求解线速度角速度之间的比例关系．
解答：解：齿轮传动中两轮不打滑，则有a、b的线速度大小相等，即υa=υb．由公式v=ωr得，ωa：ωb=rb：ra=2：1．
b、c两点角速度相同，即ωc=ωb．由公式v=ωr得，υb：υc=rb：rc=2：1．
综上得到，υa：υb：υc=2：2：1，ωa：ωb：ωc=2：1：1．
故答案为：2：2：1，2：1：1．
点评：本题是皮带传动类型的问题，关键抓住相等的条件：不打滑时，两轮边缘上各点的线速度大小相等．同一共轴转动的物体上各点的角速度相同．
解答：解：齿轮传动中两轮不打滑，则有a、b的线速度大小相等，即υa=υb．由公式v=ωr得，ωa：ωb=rb：ra=2：1．
b、c两点角速度相同，即ωc=ωb．由公式v=ωr得，υb：υc=rb：rc=2：1．
综上得到，υa：υb：υc=2：2：1，ωa：ωb：ωc=2：1：1．
故答案为：2：2：1，2：1：1．
点评：本题是皮带传动类型的问题，关键抓住相等的条件：不打滑时，两轮边缘上各点的线速度大小相等．同一共轴转动的物体上各点的角速度相同．
练习册系列答案
阅读快车系列答案
相关题目
如图是齿轮传动装置，两个齿轮的半径比ra：rb为1：2，a、b为两轮子边缘点，c 为大轮半径的中点，当齿轮转动时，
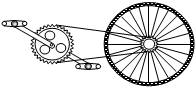如图所示是自行车传动装置的示意图，若脚蹬匀速转一圈需要时间T，已数出大齿轮齿数为48，小齿轮齿数为16，自行车后轮半径R．下列说法中正确的是（ ）| A、小齿轮、大齿轮边缘点的线速度大小之比vA：vB=3：1 | B、小齿轮、大齿轮的角速度大小之比ωA：ωB=1：3 | C、小齿轮、大齿轮的周期之比TA：TB=1：1 | D、自行车前进速度为6πR/T |
