题目内容
如图所示,质量为2kg的物体在竖直面内从半径为r=1m的 光滑圆弧最高点A由静止开始下滑,进入水平轨道MN,MN=2m,MN段粗糙且与物体的动摩擦因数为μ=0.2,则最后物体停在离M多远的地方?
光滑圆弧最高点A由静止开始下滑,进入水平轨道MN,MN=2m,MN段粗糙且与物体的动摩擦因数为μ=0.2,则最后物体停在离M多远的地方?

答案:1m
解析:
解析:
|
物体的重力势能最终全部转化为内能,因此,可以对整个过程运用能量转化与守恒定律. 解:物体从最高点由静止开始下滑到最后停在水平轨道上 P点,由能量守恒定律,有mgr=μmgs所以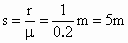 ,即P点最后离M点为1m(来回各一次后向右运动到P点). ,即P点最后离M点为1m(来回各一次后向右运动到P点).
1 .能量守恒定律应从下面两方面去理解(1) 某种形式的能减少,一定存在其他形式的能增加,且减少量和增加量一定相等.(2) 某个物体的能量减少,一定存在其他物体的能量增加,且减少量和增加量一定相等,这也是我们列能量守恒定律方程式的两条基本思路.2 .用能量守恒定律解题的步骤(1) 分清有多少种形式的能(如动能、势能、内能、电能)在变化.(2) 分别列出减少的能量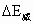 和增加的能量 和增加的能量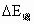 的表示式. 的表示式.
(3) 列恒等式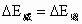 . .
3 .机械能守恒定律与能量转化和守恒定律的区别机械能守恒定律反映的是一个系统中只有重力和弹力做功,系统内物体的重力势能、弹性势能量与动能可以相互转化,但总的机械能保持不变. 能量的转化守恒定律反映的一个系统有机械能损失,但损失的机械能转变成其他形式的能,例如一个系统内有相互作用的滑动摩擦力,那么一对滑动摩擦力做功的结果,使系统的机械能减少,并进一步转化为系统的内能,系统的总能量 (包括机械能在内)是一定的. |

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
 (2011?郑州模拟)如图所示,A、B两球完全相同,质量均为m,用两根等长的细线,悬挂在升降机的天花板上的O点,两球之间连着一根劲度系数为k的轻质弹簧.当升降机以加速度a竖直向上加速运动时,两根细线之间的夹角为θ.则弹簧的长度与原长相比缩短了( )
(2011?郑州模拟)如图所示,A、B两球完全相同,质量均为m,用两根等长的细线,悬挂在升降机的天花板上的O点,两球之间连着一根劲度系数为k的轻质弹簧.当升降机以加速度a竖直向上加速运动时,两根细线之间的夹角为θ.则弹簧的长度与原长相比缩短了( ) (1)在做“用单摆测定重力加速度”的实验中,有人提出以下几点建议:
(1)在做“用单摆测定重力加速度”的实验中,有人提出以下几点建议: ,量程为1mA,内阻rg约为100Ω.要求测量其内阻.可选用的器材有:电阻箱R0,最大阻值为99999.9Ω;滑动变阻器甲,最大阻值为10kΩ;滑动变阻器乙,最大阻值为2kΩ;电源E1,电动势约为2V,内阻不计;电源E2,电动势约为6V,内阻不计;开关2个,导线若干.
,量程为1mA,内阻rg约为100Ω.要求测量其内阻.可选用的器材有:电阻箱R0,最大阻值为99999.9Ω;滑动变阻器甲,最大阻值为10kΩ;滑动变阻器乙,最大阻值为2kΩ;电源E1,电动势约为2V,内阻不计;电源E2,电动势约为6V,内阻不计;开关2个,导线若干. 满偏;c.合上S2,调节R1使
满偏;c.合上S2,调节R1使 半偏,此时可认为的
半偏,此时可认为的 的内阻rg=R1.试问:
的内阻rg=R1.试问: (1)下列说法正确的是
(1)下列说法正确的是 与劲度系数为K的轻质弹簧连接,右端与劲度系数为2K的轻质弹簧连接,左右两弹簧原长均为L0,弹簧的另一端均固定在墙壁上.将物体拉离平衡位置,放手后,物体在光滑水平面上往复运动,证明物体的运动是简谐运动并求简谐运动的平衡位置.
与劲度系数为K的轻质弹簧连接,右端与劲度系数为2K的轻质弹簧连接,左右两弹簧原长均为L0,弹簧的另一端均固定在墙壁上.将物体拉离平衡位置,放手后,物体在光滑水平面上往复运动,证明物体的运动是简谐运动并求简谐运动的平衡位置. (1)有一游标卡尺,主尺的最小分度是1mm,游标上有20个小的等分刻度.用它测量一小球的直径,如图1所示的读数是
(1)有一游标卡尺,主尺的最小分度是1mm,游标上有20个小的等分刻度.用它测量一小球的直径,如图1所示的读数是
 一有界匀强磁场区域如图所示,质量为m、电阻为R的长方形矩形线圈abcd边长分别为L和2L,线圈一半在磁场内,一半在磁场外,t0时刻磁场开始均匀减小,磁感强度B随时间t的变化关系为B=B0-kt,线圈中产生感应电流,仅在磁场力作用下从静止开始运动,求:
一有界匀强磁场区域如图所示,质量为m、电阻为R的长方形矩形线圈abcd边长分别为L和2L,线圈一半在磁场内,一半在磁场外,t0时刻磁场开始均匀减小,磁感强度B随时间t的变化关系为B=B0-kt,线圈中产生感应电流,仅在磁场力作用下从静止开始运动,求: