题目内容
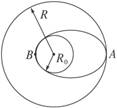
飞船沿半径为R的圆周绕地球运动,如图所示,其周期为T,如果飞船要返回地面,可在轨道上某一点A处将速率降低到适当数值,从而使飞船沿着以地心为焦点的椭圆轨道运行,椭圆和地球表面相切于B点,设地球半径为R0,问飞船从A点返回到地面上B点所需时间为多少?
【答案】
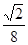 (1+
(1+ T
T
【解析】飞船返回时间为椭圆运行周期T′的一半,而椭圆的长半轴为 (R+R0),
(R+R0),
由开普勒第三定律可得
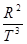 =
=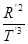
所以t= T′=
T′=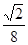 (1+
(1+ T.
T.
思路分析:开普勒定律虽是对太阳行星系统而言的,但该定律也适合于地球卫星系统,飞船返回时是以地心为焦点的椭圆轨道运行,那么应用开普勒第三定律可求返回时间
试题点评:对于绕同一个中心天体运动的星体都可以运用开普勒第三定律研究半径,周期关系

练习册系列答案
相关题目
 飞船沿半径为R的圆周绕地球运动,其周期为T,如果飞船要返回地面,可在轨道上的某一点A处,将速率降低到适当数值,从而使飞船沿着以地心为焦点的特殊椭圆轨道运动,椭圆和地球表面在B点相切,如图所示,如果地球半径为r,且R=3r,则飞船由A点到B点所需的时间
飞船沿半径为R的圆周绕地球运动,其周期为T,如果飞船要返回地面,可在轨道上的某一点A处,将速率降低到适当数值,从而使飞船沿着以地心为焦点的特殊椭圆轨道运动,椭圆和地球表面在B点相切,如图所示,如果地球半径为r,且R=3r,则飞船由A点到B点所需的时间


