题目内容
质量分别为mA=2.0kg,mB=1.0kg的A、B两物体,在光滑的水平面上沿同一条直线运动.当它们相距9.0m时开始计时,经过5.0s,B追上A,两物碰撞后合为一体,仍沿直线前进.这时它们的动能为6.0J,求:它们碰撞过程中损失的机械能.
分析:AB碰撞过程中动量守恒,根据动量守恒定律及运动学公式求出共同速度,再根据能量守恒定律求出碰撞过程中损失的机械能.
解答:解:设A、B两物体原来的速度分别为vA和vB
则有:vBt-vAt=s ①
由动量守恒定律得:
mAvA+mBvB=(mA+mB)v共 ②
(mA+mB)
=6J ③
由能量关系有:
mA
+
mB
-
(mA+mB)
=E损④
由①②③④解得:
E损=1.08J
答:它们碰撞过程中损失的机械能为1.08J
则有:vBt-vAt=s ①
由动量守恒定律得:
mAvA+mBvB=(mA+mB)v共 ②
| 1 |
| 2 |
| v | 2 共 |
由能量关系有:
| 1 |
| 2 |
| v | 2 A |
| 1 |
| 2 |
| v | 2 A |
| 1 |
| 2 |
| v | 2 共 |
由①②③④解得:
E损=1.08J
答:它们碰撞过程中损失的机械能为1.08J
点评:本题主要考查了动量守恒定律及能量守恒定律的直接应用,难度适中.

练习册系列答案
 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
 [物理-选修3-5]
[物理-选修3-5] (1)2011年3月,日本地震引发海啸,继而福岛核电站(世界最大的核电站)发生核泄漏.关于核电站和核辐射,下列说法中正确的是
(1)2011年3月,日本地震引发海啸,继而福岛核电站(世界最大的核电站)发生核泄漏.关于核电站和核辐射,下列说法中正确的是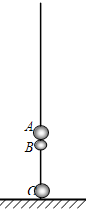 如图所示,均可视为质点的三个物体A、B、C穿在竖直固定的光滑绝缘细线上,A与B紧靠在一起(但不粘连),C紧贴着绝缘地板,质量分别为MA=2.32kg,MB=0.20kg,MC=2.00kg,其中A不带电,B、C的带电量分别为qB=+4.0×10-5c,qC=+7.0×10-5c,且电量都保持不变,开始时三个物体均静止.现给物体A施加一个竖直向上的力F,若使A由静止开始向上作加速度大小为a=4.0m/s2的匀加速直线运动,则开始需给物体A施加一个竖直向上的变力F,经时间t 后,F变为恒力.已知g=10m/s2,静电力恒量k=9×109N?m2/c2,求:
如图所示,均可视为质点的三个物体A、B、C穿在竖直固定的光滑绝缘细线上,A与B紧靠在一起(但不粘连),C紧贴着绝缘地板,质量分别为MA=2.32kg,MB=0.20kg,MC=2.00kg,其中A不带电,B、C的带电量分别为qB=+4.0×10-5c,qC=+7.0×10-5c,且电量都保持不变,开始时三个物体均静止.现给物体A施加一个竖直向上的力F,若使A由静止开始向上作加速度大小为a=4.0m/s2的匀加速直线运动,则开始需给物体A施加一个竖直向上的变力F,经时间t 后,F变为恒力.已知g=10m/s2,静电力恒量k=9×109N?m2/c2,求: