题目内容
质量为 0.5kg的物体由静止开始沿光滑斜面下滑,下滑到斜面的底端后进入粗糙水平面滑行,直到静止,它的v-t图象如图所示.(g取10m/s2),求:①斜面的倾角
②物体与水平面的动摩擦因数
③摩擦阻力做的功.
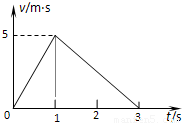
【答案】分析:①物块先在光滑斜面上做匀加速,后在粗糙水平面上做匀减速.由图象的斜率可求得下滑的加速度,从而可求出斜面倾角.
②由图象可知匀减速的时间与速度变化,从而求出加速度的大小,由牛顿第二定律可算出滑动摩擦力大小,并求出物体与水平面的动摩擦因数.
③对于匀减速运动过程,运用动能定理求解摩擦阻力做的功.
解答:解:(1)由图可知,物体在斜面的加速度为 =5m/s2
=5m/s2
又由牛顿第二定律得 ma=mgsinθ 所以 θ=30°
(2)物体在水平面的加速度为a2= =
=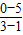 =-2.5m/s2
=-2.5m/s2
由牛顿第二定律得ma2=μmg
解得μ=0.25
(3)对匀减速运动过程,由动能定理得
 =-6.25J
=-6.25J
答:①斜面的倾角是30°.
②物体与水平面的动摩擦因数是0.25.
③摩擦阻力做的功为-6.25J.
点评:本题主要考查了牛顿第二定律和动能定理的应用,关键要抓住加速度的大小可由图象的斜率大小来表示.
②由图象可知匀减速的时间与速度变化,从而求出加速度的大小,由牛顿第二定律可算出滑动摩擦力大小,并求出物体与水平面的动摩擦因数.
③对于匀减速运动过程,运用动能定理求解摩擦阻力做的功.
解答:解:(1)由图可知,物体在斜面的加速度为
 =5m/s2
=5m/s2又由牛顿第二定律得 ma=mgsinθ 所以 θ=30°
(2)物体在水平面的加速度为a2=
 =
=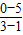 =-2.5m/s2
=-2.5m/s2由牛顿第二定律得ma2=μmg
解得μ=0.25
(3)对匀减速运动过程,由动能定理得
 =-6.25J
=-6.25J答:①斜面的倾角是30°.
②物体与水平面的动摩擦因数是0.25.
③摩擦阻力做的功为-6.25J.
点评:本题主要考查了牛顿第二定律和动能定理的应用,关键要抓住加速度的大小可由图象的斜率大小来表示.

练习册系列答案
相关题目
 如图,斜面和水平面由一小段光滑圆弧连接,斜面的倾角为37°,一质量为0.5kg的物块从距斜面底端5m处的A点由静止释放,已知物块和斜面及水平面间的动摩擦因数均为0.3(sin37°=0.6,cos37°=0.8,g=10m/s2)
如图,斜面和水平面由一小段光滑圆弧连接,斜面的倾角为37°,一质量为0.5kg的物块从距斜面底端5m处的A点由静止释放,已知物块和斜面及水平面间的动摩擦因数均为0.3(sin37°=0.6,cos37°=0.8,g=10m/s2)