题目内容
13．
射箭的弓顶部跨度为l，弦均匀且弹性良好，其自由长度为l，发射时弦和箭可等效为右图乙的情景，假设弓的跨度保持不变．已知弦的劲度系数为k，发射箭时弦的最大长度为$\frac{5}{3}$l（弹性限度内），则箭被发射瞬间所受的最大弹力为（设弦的弹力满足胡克定律）（ ）| A． | kl | B． | $\frac{16}{15}$kl | C． | $\sqrt{3}$kl | D． | 2kl |
分析 力的合成遵循力的平行四边形定则，由题意可结合等边三角形的几何知识求解合力．
解答 解：设放箭处弦的弹力分别为F1、F2，合力为F，则有：F1=F2=k（$\frac{5}{3}$l-l）=$\frac{2}{3}$kl，F=2F1•cosθ，
由几何关系得：sinθ=$\frac{\frac{l}{2}}{\frac{5l}{6}}$=$\frac{3}{5}$，得：cosθ=$\frac{4}{5}$，
所以，箭被发射瞬间所受的最大弹力F=$\frac{16}{15}kl$，故ACD错误，B正确．
故选：B．
点评 本题考查力的合成平行四边形定则，结合图形利用等边三角形的知识容易解决，会用合力的大小公式也可以解决，可灵活处理．
练习册系列答案
相关题目
3．
如图所示，轻弹簧上端固定在天花板上，下端悬挂木块A，A处于静止状态，测得此时弹簧的长度为x（弹簧的形变在弹性限度内）．已知木块A的质量为m，重力加速度为g，则此弹簧的劲度系数应该（ ）
如图所示，轻弹簧上端固定在天花板上，下端悬挂木块A，A处于静止状态，测得此时弹簧的长度为x（弹簧的形变在弹性限度内）．已知木块A的质量为m，重力加速度为g，则此弹簧的劲度系数应该（ ）| A． | 大于$\frac{mg}{x}$ | B． | 小于$\frac{x}{mg}$ | C． | 小于mgx | D． | 等于$\frac{1}{mgx}$ |
4．如图所示，ab间接电压恒定的交变电源，M为理想变压器，如果R1的阻值增大，则（ ）
| A． | 电压表示数增大 | B． | 电流表的示数增大 | ||
| C． | 灯泡L的亮度变暗 | D． | 电阻R2的热功率增大 |
如图所示，在距离水平地面h=0.8m的虚线的上方，有一个方向垂直于纸面水平向内的匀强磁场B=1T．正方形线框abcd的边长l=0.2m，质量m=0.1kg．一条不可伸长的轻绳绕过轻滑轮，一端连线框，另一端连一质量M=0.2kg的物体A．开始时线框的cd在地面上，各段绳都处于伸直状态，从如图所示的位置由静止释放物体A，一段时间后线框进入磁场运动，已知线框的ab边刚进入磁场时线框恰好做匀速运动．当线框的cd边进入磁场时物体A恰好落地，同时将轻绳剪断，线框继续上升一段时间后开始下落．整个过程线框没有转动，线框平面始终处于纸面内，g取10m/s2．求：
8．关于原子及原子核，以下说法正确的是（ ）
| A． | 天然放射现象揭示了原子是可以再分的 | |
| B． | 某放射性元素的原子核发生了一次a衰变，则其质子数减小2 | |
| C． | β射线为原子的核外电子电离后形成的电子流 | |
| D． | 氢原子从高能级向低能级跃迁的过程中会辐射一定频率的光子 |
18．在“描绘小灯泡的伏安特性曲线”实验中，要测量一个标有“2.7V 1.5W”的灯泡两端的电压和通过它的电流，现有如下器材：
A．直流电源3V（内阻可不计） B．直流电表0～3A（内阻约0.1Ω）
C．直流电表0～0.6A（内阻约0.5Ω） D．直流电压表0～3V（内阻约3kΩ）
E．直流电压表0～15V（内阻约200kΩ） F．滑动变阻器（10Ω，1A）
G．滑动变阻器（1kΩ，300mA）
①除开关、导线外，为完成实验，需要从上述器材中选用ACDF（用字母）
②某几位同学设计了如下A、B、C、D所示的电路图，正确的是D；并根据正确的电路图在实物图中正确连好线．
③表中的各组数据该同学在实验中测得的，根据表格中的数据在图所示的方格纸上已经描好点，请作出该灯泡的伏安特性曲线，根据该曲线可以判断：随电压的增大，灯泡的电阻增大．
A．直流电源3V（内阻可不计） B．直流电表0～3A（内阻约0.1Ω）
C．直流电表0～0.6A（内阻约0.5Ω） D．直流电压表0～3V（内阻约3kΩ）
E．直流电压表0～15V（内阻约200kΩ） F．滑动变阻器（10Ω，1A）
G．滑动变阻器（1kΩ，300mA）
①除开关、导线外，为完成实验，需要从上述器材中选用ACDF（用字母）
②某几位同学设计了如下A、B、C、D所示的电路图，正确的是D；并根据正确的电路图在实物图中正确连好线．
③表中的各组数据该同学在实验中测得的，根据表格中的数据在图所示的方格纸上已经描好点，请作出该灯泡的伏安特性曲线，根据该曲线可以判断：随电压的增大，灯泡的电阻增大．
| U/V | I/A |
| 0 | 0 |
| 0.5 | 0.17 |
| 1.0 | 0.30 |
| 1.5 | 0.39 |
| 2.0 | 0.45 |
| 2.5 | 0.49 |
在“探究力的平行四边形定则”的实验中，首先用两个弹簧秤分别勾住绳套，在保证弹簧秤与木板平行的条件下，互成角度地拉长橡皮条，使结点到达O点，用铅笔记下0点位置及两细绳的方向，如图中的OA、OB方向，读出两弹簧秤的示数F0A=2.7N、F0B=3.3N．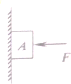
如图 6--4所示，在F作用下，质量为10kg的物体A静止在竖直墙上，这时F=50N，如果F增大为100N，A还静止在墙上，在这两种情况下，A所受到的摩擦力如何变化？（g取10m/s2）