题目内容
18. 如图所示,真空室内有一个点状的α粒子放射源P,它向各个方向发射α粒子(不计重力),速率都相同.ab为P点附近的一条水平直线(P到直线ab的距离PC=L),Q为直线ab上一点,它与P点相距PQ=$\frac{{\sqrt{5}}}{2}L$(现只研究与放射源P和直线ab同一个平面内的α粒子的运动),当真空室内(直线ab以上区域)只存在垂直该平面向里、磁感应强度为B的匀强磁场时,水平向左射出的α粒子恰到达Q点;当真空室(直线ab以上区域)只存在平行该平面的匀强电场时,不同方向发射的α粒子若能到达ab直线,则到达ab直线时它们动能都相等,已知水平向左射出的α粒子也恰好到达Q点.(α粒子的电荷量为+q,质量为m;sin37°=0.6;cos37°=0.8)求:
如图所示,真空室内有一个点状的α粒子放射源P,它向各个方向发射α粒子(不计重力),速率都相同.ab为P点附近的一条水平直线(P到直线ab的距离PC=L),Q为直线ab上一点,它与P点相距PQ=$\frac{{\sqrt{5}}}{2}L$(现只研究与放射源P和直线ab同一个平面内的α粒子的运动),当真空室内(直线ab以上区域)只存在垂直该平面向里、磁感应强度为B的匀强磁场时,水平向左射出的α粒子恰到达Q点;当真空室(直线ab以上区域)只存在平行该平面的匀强电场时,不同方向发射的α粒子若能到达ab直线,则到达ab直线时它们动能都相等,已知水平向左射出的α粒子也恰好到达Q点.(α粒子的电荷量为+q,质量为m;sin37°=0.6;cos37°=0.8)求:(1)α粒子的发射速率;
(2)匀强电场的场强大小和方向;
(3)当仅加上述磁场时,能到达直线ab的α粒子所用最长时间和最短时间的比值.
分析 (1)当只存在匀强磁场时,α粒子由洛伦兹力提供向心力而做匀速圆周运动,画出α粒子的运动轨迹,由几何知识求出α粒子做匀速圆周运动的半径,由牛顿第二定律求出α粒子的发射速率;
(2)当只存在匀强电场时,α粒子做类平抛运动,由牛顿第二定律和运动学结合求解匀强电场的场强大小、方向;
(3)当仅加上述磁场时,根据几何知识确定出轨迹的圆心角,然后求出时间.
解答 解:(1)设α粒子做匀速圆周运动的半径R,过O作PQ的垂线交PQ于A点,如图所示,
由几何知识可得:$\frac{{\overline{PC}}}{{\overline{PQ}}}=\frac{{\overline{QA}}}{{\overline{QO}}}$,
代入数据可得α粒子轨迹半径:$R=\overline{QO}=\frac{5L}{8}$,
洛仑磁力提供向心力:$Bqυ=m\frac{υ^2}{R}$,解得α粒子发射速度为:$υ=\frac{5BqL}{8m}$;
(2)真空室只加匀强电场时,由α粒子到达ab直线的动能相等,可得ab为等势面,电场方向垂直ab向下.
水平向左射出的α粒子做类平抛运动,由运动学关系可知:
与ab平行方向:$\overline{CQ}=\frac{L}{2}=υt$,
与ab垂直方向:$\overline{PC}=L=\frac{1}{2}a{t^2}$,
其中$a=\frac{Eq}{m}$,
解得:$E=\frac{{25qL{B^2}}}{8m}$;
(3)真空室只加磁场时,圆弧O1和直线ab相切于D点,α粒子转过的圆心角最大,运动时间最长,如图所示.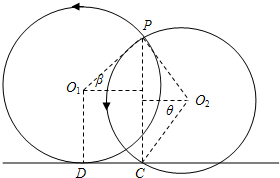
则:$sinβ=\frac{L-R}{R}$=$\frac{3}{5}$,β=37°,
最大圆心角:γmax=360°-90°-37°=233°,
最长时间:${t_1}=\frac{{{γ_{max}}}}{360°}T$,
圆弧O2经C点,α粒子转过的圆心角最小,运动时间最短.
则:$sinθ=\frac{L/2}{R}$=$\frac{4}{5}$(1分)θ=53°,
最小圆心角:γmin=2θ=106°,
最短时间:${t_2}=\frac{{{γ_{min}}}}{360°}T$,
则最长时间和最短时间的比值为:$\frac{t_1}{t_2}=\frac{{{γ_{max}}}}{{{γ_{min}}}}=\frac{233}{106}$(或2.20);
答:(1)α粒子的发射速率为$\frac{5BqL}{8m}$;
(2)匀强电场的场强大小为$\frac{25qL{B}^{2}}{8m}$,方向:垂直ab向下;
(3)当仅加上述磁场时,能到达直线ab的α粒子所用最长时间和最短时间的比值为$\frac{233}{106}$.
点评 本题的突破口是确定α粒子在匀强磁场中和匀强电场中的运动轨迹,由几何知识求解磁场中圆周运动的半径.

 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案| A. | v=4.5m/s,a=0 | B. | v=4.5m/s,a=1.5m/s2 | ||
| C. | v=7.5m/s,a=0 | D. | v=7.5m/s,a=1.5m/s2 |
 如图所示,在竖直放置的金属板M上放一个放射源C,可向纸面内各个方向射出速率均为v的α粒子,P是与金属板M 平行的足够大的荧光屏,到M的距离为d.现在 P与金属板M间加上垂直纸面的匀强磁场,调整磁感应强度的大小,恰使沿M板向上射出的α粒子刚好垂直打在荧光屏上.若α粒子的质量为m,电荷量为2e.则( )
如图所示,在竖直放置的金属板M上放一个放射源C,可向纸面内各个方向射出速率均为v的α粒子,P是与金属板M 平行的足够大的荧光屏,到M的距离为d.现在 P与金属板M间加上垂直纸面的匀强磁场,调整磁感应强度的大小,恰使沿M板向上射出的α粒子刚好垂直打在荧光屏上.若α粒子的质量为m,电荷量为2e.则( )| A. | 磁场方向垂直纸面向里,磁感应强度B的大小为$\frac{2mv}{ed}$ | |
| B. | 磁场方向垂直纸面向外,磁感应强度B的大小为$\frac{mv}{2ed}$ | |
| C. | 在荧光屏上能观察到的亮斑区的长度为2d | |
| D. | 在荧光屏上能观察到的亮斑区的长度为3d |

| A. | 0、0、0 | B. | 0、1、0 | C. | 1、0、0 | D. | 1、1、1 |
 如图所示,物块P质量为M,位于水平粗糙桌面上(动摩擦因数为μ),用跨过光滑轻质定滑轮的轻绳将P与小盘相连,小盘内有砝码,小盘与砝码的总质量为m,在P向右运动的过程中,桌面以上的绳子始终是水平的,关于物体P受到的拉力和摩擦力的以下描述中正确的是( )
如图所示,物块P质量为M,位于水平粗糙桌面上(动摩擦因数为μ),用跨过光滑轻质定滑轮的轻绳将P与小盘相连,小盘内有砝码,小盘与砝码的总质量为m,在P向右运动的过程中,桌面以上的绳子始终是水平的,关于物体P受到的拉力和摩擦力的以下描述中正确的是( )| A. | 若P匀速运动,则其受到的拉力大小等于mg | |
| B. | 若P加速运动,则其受到的拉力大小等于mg | |
| C. | 若P匀速运动,则其受到的摩擦力大小一定等于μmg | |
| D. | 若P加速运动,则其受到的摩擦力大小一定等于mg |
 如图所示.平行金属带电极板A、B间可看成匀强电场,场强E=1.2×102V/m,极板间距离d=5cm,电场中C和D点分别到A、B两板的距离均为0.5cm,B板接地,则:
如图所示.平行金属带电极板A、B间可看成匀强电场,场强E=1.2×102V/m,极板间距离d=5cm,电场中C和D点分别到A、B两板的距离均为0.5cm,B板接地,则: 如图所示,轻杆长为L=1.5m,可绕无摩擦的转动,在杆上距离轴O点$\frac{L}{3}$的A点和端点B各固定一质量均为m=1kg的小球,使杆从水平位置无初速释放摆下.求当杆转到竖直位置时,
如图所示,轻杆长为L=1.5m,可绕无摩擦的转动,在杆上距离轴O点$\frac{L}{3}$的A点和端点B各固定一质量均为m=1kg的小球,使杆从水平位置无初速释放摆下.求当杆转到竖直位置时,