题目内容
如图所示，水平绝缘轨道
与处于竖直平面内的半圆形绝缘光滑轨道
平滑连接，半圆形轨道的半径
。轨道所在空间存在水平向右的匀强电场，电场强度
。现有一电荷量
，质量
的带电体(可视为质点)，在水平轨道上的
点由静止释放，已知点与圆形轨道最低点
距离
.带电体与水平轨道间的动摩擦因数
,重力加速度
，取
.求：
(1)带电体运动到圆形轨道的最高点
时，速度的大小？
(2)带电体第一次经过点后，落在水平轨道上的位置到点的距离？
(3)带电体在轨道上运动对轨道能产生的最大压力大小？
【答案】
（1）
（2）
（3）
【解析】
试题分析：（1）在水平轨道上时滑动摩擦力为
，电场力为
，所以在运动过程中加速度为
，所以到达B时其速度为
即
。
从B到C根据动能定理则
，所以
（2）从C出发后竖直方向自由落体，水平方向匀加速直线运动，则
则
，则
（3）最大压力应该在与竖直方向夹角为
处，即
则
通过上述方程求解则，当角度为45°时，支持力取得最大值，即8.45N
考点：动能定理、圆周运动知识
点评：本题考查了通过动能定理求速度以及通过圆周运动、结合数理知识分析取得最大值的条件。
练习册系列答案
文敬图书课时先锋系列答案
相关题目
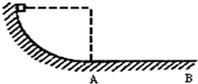如图所示，质量为0.2Kg的物体带电量为1×10-3C，从半径为0.45m的光滑的1/4圆弧的绝缘滑轨上端由静止下滑到底端，然后继续沿水平面滑动．
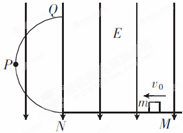（2011?安徽模拟）如图所示，在E=1×103V/m的竖直匀强电场中，有一光滑的半圆形绝缘轨QPN与一水平绝缘轨道MN连接，半圆形轨道平面与电场线平行，P为QN圆弧的中点，其半径R=40cm，一带正电q=10-4C的小滑块质量m=10g，与水平轨道间的动摩擦因数μ=0.15，位于N点右侧1.5m处，取g=10m/s2，求：
如图所示，一根水平光滑的绝缘直槽轨连接一个竖直放置的半径为R=0.50m的绝缘光滑槽轨．槽轨处在垂直纸面向外的匀强磁场中，磁感应强度B=0.50T．有一个质量m=0.10g，带电量为q=+1.6×10-3C的小球在水平轨道上向右运动．若小球恰好能通过最高点，重力加速度g=10m/s2．试求：
如图所示，在竖直向下的匀强电场中有一绝缘的光滑轨道，一个带负电的小球从斜轨上的A点由静止释放，沿轨道滑下，已知小球的质量为m，电荷量为-q，匀强电场的场擞大小为E，斜轨道的倾角为a，圆轨迹道半径为R，小球的重力大于受的电场力．
（2007?湖北模拟）如图所示，一根水平光滑的绝缘直槽轨连接一个竖直放置的半径为R=0.50m的绝缘光滑槽轨．槽轨处在垂直纸面向外的匀强磁场中，磁感应强度B=0.50T．有一个质量m=0.10g，带电量为q=+1.6×10-3C的小球在水平轨道上向右运动．若小球恰好能通过最高点，则下列说法正确的是（ ）