题目内容
在一个边长为a的等边三角形区域内分布着磁感应强度为B的匀强磁强，一质量为 m、电荷量为q的带电粒子从BC边的中点垂直BC方向射入磁场中，如图所示，为使该粒子能从AB边（或AC边）射出，则带电粒子的初速度v必须大于分析：本题粒子的半径确定，圆心必定在BC直线上，当轨迹与AB相切时为临界情况，画出轨迹图，由几何知识确定半径的大小，然后根据牛顿第二定律列方程表示出v，代入r即可求解．
解答：解：如图当粒子运动轨迹与AB相切时为临界情况：
设此时粒子半径为r，由几何知识可得：
+r=
解得：r=
根据牛顿第二定律qvB=m
得：v=
=
v必须大于此值．
故答案为：
．
设此时粒子半径为r，由几何知识可得：
| 2r | ||
|
| a |
| 2 |
解得：r=
| ||
2(2+
|
根据牛顿第二定律qvB=m
| v2 |
| r |
得：v=
| qBr |
| m |
qBa
| ||
2m(2+
|
v必须大于此值．
故答案为：
qBa
| ||
2m(2+
|
点评：考查带电粒子在匀强磁场中的匀速圆周运动，关键是找到相切的临界情况后由几何知识确定轨道半径．
练习册系列答案
口算题卡加应用题集训系列答案
相关题目
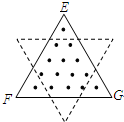（2013?虹口区二模）如图所示，在边长为a的等边三角形区域内有匀强磁场B，其方向垂直纸面向外，一个边长也为a的等边三角形导线框架EFG正好与上述磁场区域的边界重合，现使导线框以周期T绕其中心O点在纸面内匀速转动，经过
用三根轻杆做成一个边长为L的等边三角形的框架，在其中两个顶点处各固定一个小球A和B，质量分别为2m和m．现将三角形框架的第三个顶点悬挂在天花板上O点，框架可绕O点自由转动．有一水平方向的力F作用在小球A上，使OB间的杆恰好静止于竖直方向，现将F撤去，则力F的大小以及撤去F后A球运动到最低点时的速度大小分别为（ ）A、
| ||||||||
B、2
| ||||||||
C、2
| ||||||||
D、
|
