题目内容
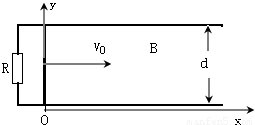
如图所示,两根相距为d的足够长的平行金属导轨位于水平的xy平面内,一端接有阻值为R的电阻.在x>0的一侧存在沿垂直纸面方向的均匀磁场,磁感强度B随x的增大而增大,B=kx,式中的k是一常量,一金属直杆与金属导轨垂直,可在导轨上无摩擦的滑动,当t=0时位于x=0处,速度为v,方向沿x轴的正方向.在运动过程中,有一大小可调节的外力F作用于金属杆以保持金属杆的加速度恒定,大小为a,方向沿x轴的负方向.设除外接的电阻R外,所有其它电阻都可以忽略.问:(1)该回路中的感应电流持续的时间多长?
?(2)当金属杆的速度大小为v/2时,回路中的感应电动势有多大?
【答案】分析:(1)回路中有感应电流的时间是向右做匀减速直线运动到零然后返回做匀加速直线运动到离开磁场的时间,结合运动学公式求出感应电流持续的时间.
(2)根据匀变速直线运动的速度位移公式求出速度减为 经过的位移,从而得出此时的磁感应强度大小,结合切割产生的感应电动势公式求出回路中的感应电动势大小.
经过的位移,从而得出此时的磁感应强度大小,结合切割产生的感应电动势公式求出回路中的感应电动势大小.
解答:解:(1)金属杆在导轨上先是向右做加速度为a的匀减速直线运动,运动到导轨右方最远处速度为零.然后,又沿导轨向左做加速度为a的匀加速直线运动.当过了原点O后,由于已离开了磁场区,故回路中不再有感应电流.因而该回路中感应电流持续的时间就等于金属杆从原点O向右运动到最远处,再从最远处向左运动回到原点O的时间,这两段时间是相等的.以t1表示金属杆从原点O到右方最远处所需的时间,则由运动学公式得 v-at1=0,
?由上式解出t1,就得知该回路中感应电流持续的时间 T= .
.
?(2)以x1表示金属杆的速度变为v1= v时它所在的x坐标,对于匀减速直线运动有
v时它所在的x坐标,对于匀减速直线运动有
?v12=v2-2ax1,
?以v1= v代入就得到此时金属杆的x坐标,即
v代入就得到此时金属杆的x坐标,即
?x1=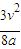 .
.
?由题给条件就得出此时金属杆所在处的磁感应强度B=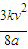
?因而此时由金属杆切割磁感线产生的感应电动势
?E1=Bv1l= .
.
答:(1)该回路中的感应电流持续的时间为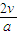 .
.
(2)回路中的感应电动势为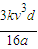 .
.
点评:解决本题的关键知道回路中有感应电流的过程,结合切割产生的感应电动势公式、运动学公式进行求解.
(2)根据匀变速直线运动的速度位移公式求出速度减为
 经过的位移,从而得出此时的磁感应强度大小,结合切割产生的感应电动势公式求出回路中的感应电动势大小.
经过的位移,从而得出此时的磁感应强度大小,结合切割产生的感应电动势公式求出回路中的感应电动势大小.解答:解:(1)金属杆在导轨上先是向右做加速度为a的匀减速直线运动,运动到导轨右方最远处速度为零.然后,又沿导轨向左做加速度为a的匀加速直线运动.当过了原点O后,由于已离开了磁场区,故回路中不再有感应电流.因而该回路中感应电流持续的时间就等于金属杆从原点O向右运动到最远处,再从最远处向左运动回到原点O的时间,这两段时间是相等的.以t1表示金属杆从原点O到右方最远处所需的时间,则由运动学公式得 v-at1=0,
?由上式解出t1,就得知该回路中感应电流持续的时间 T=
 .
.?(2)以x1表示金属杆的速度变为v1=
 v时它所在的x坐标,对于匀减速直线运动有
v时它所在的x坐标,对于匀减速直线运动有?v12=v2-2ax1,
?以v1=
 v代入就得到此时金属杆的x坐标,即
v代入就得到此时金属杆的x坐标,即?x1=
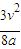 .
.?由题给条件就得出此时金属杆所在处的磁感应强度B=
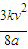
?因而此时由金属杆切割磁感线产生的感应电动势
?E1=Bv1l=
 .
.答:(1)该回路中的感应电流持续的时间为
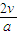 .
.(2)回路中的感应电动势为
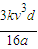 .
.点评:解决本题的关键知道回路中有感应电流的过程,结合切割产生的感应电动势公式、运动学公式进行求解.

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
 (2005?辽宁)如图所示,两根相距为l的平行直导轨ab、cd、b、d间连有一固定电阻R,导轨电阻可忽略不计.MN为放在ab和cd上的一导体杆,与ab垂直,其电阻也为R.整个装置处于匀强磁场中,磁感应强度的大小为B,磁场方向垂直于导轨所在平面(指向图中纸面内).现对MN施力使它沿导轨方向以速度v(如图)做匀速运动.令U表示MN两端电压的大小,则( )
(2005?辽宁)如图所示,两根相距为l的平行直导轨ab、cd、b、d间连有一固定电阻R,导轨电阻可忽略不计.MN为放在ab和cd上的一导体杆,与ab垂直,其电阻也为R.整个装置处于匀强磁场中,磁感应强度的大小为B,磁场方向垂直于导轨所在平面(指向图中纸面内).现对MN施力使它沿导轨方向以速度v(如图)做匀速运动.令U表示MN两端电压的大小,则( )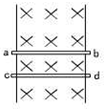 如图所示,两根相距为L的竖直平行金属导轨位于匀强磁场中,磁感应强度为B,导轨电阻不计,另两根与光滑轨道接触的金属杆质量均为m,电阻均为R,若要使cd杆恰好平衡,且静止不动,则ab杆应做
如图所示,两根相距为L的竖直平行金属导轨位于匀强磁场中,磁感应强度为B,导轨电阻不计,另两根与光滑轨道接触的金属杆质量均为m,电阻均为R,若要使cd杆恰好平衡,且静止不动,则ab杆应做 如图所示,两根相距为L的竖直固定杆上各套有质量为m的小球,小球可以在杆上无摩擦地自由滑动,两球用长为2L的轻绳相连,今在轻绳中点施加一个竖直向上的拉力F,恰能使两球沿竖直杆向上匀速运动.则每个小球所受的拉力大小为(重力加速度为g)( )
如图所示,两根相距为L的竖直固定杆上各套有质量为m的小球,小球可以在杆上无摩擦地自由滑动,两球用长为2L的轻绳相连,今在轻绳中点施加一个竖直向上的拉力F,恰能使两球沿竖直杆向上匀速运动.则每个小球所受的拉力大小为(重力加速度为g)( ) (2005?海淀区一模)如图所示,两根相距为d足够长的平行光滑金属导轨位于水平面的xoy平面内,一端接有阻值为R的电阻.在x>0的一侧存在竖直向下的匀强磁场,磁感应强度为B,一电阻为r的金属直杆与金属导轨垂直放置并接触良好,金属杆可在导轨上滑动.开始时,金属直杆位于x=0处,给金属杆一大小为v0、方向沿x轴正方向的初速度.在运动过程中有一大小可调节的外力F作用在金属杆上,使金属杆保持大小为a、方向沿x轴负方向的恒定加速度运动.金属轨道电阻忽略不计.
(2005?海淀区一模)如图所示,两根相距为d足够长的平行光滑金属导轨位于水平面的xoy平面内,一端接有阻值为R的电阻.在x>0的一侧存在竖直向下的匀强磁场,磁感应强度为B,一电阻为r的金属直杆与金属导轨垂直放置并接触良好,金属杆可在导轨上滑动.开始时,金属直杆位于x=0处,给金属杆一大小为v0、方向沿x轴正方向的初速度.在运动过程中有一大小可调节的外力F作用在金属杆上,使金属杆保持大小为a、方向沿x轴负方向的恒定加速度运动.金属轨道电阻忽略不计.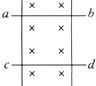 如图所示,两根相距为L的竖直平行光滑金属导轨位于磁感应强度为B、方向垂直纸面向里的匀强磁场中,导轨电阻不计,另外两根与上述导轨保持良好接触的金属杆ab、cd质量均为m,ab、cd接入闭合电路的电阻均为R,若要cd静止不动,可使ab竖直向
如图所示,两根相距为L的竖直平行光滑金属导轨位于磁感应强度为B、方向垂直纸面向里的匀强磁场中,导轨电阻不计,另外两根与上述导轨保持良好接触的金属杆ab、cd质量均为m,ab、cd接入闭合电路的电阻均为R,若要cd静止不动,可使ab竖直向