题目内容
6.某同学设计了如图(a)的装置验证小球摆动过程中的机械能守恒.实验中小球到达B点时恰好与桌面接触但没有弹力,D处的箭头处放一锋利的刀片,细线到达竖直位置时被割断,小球做平抛运动落到地面,P是一刻度尺.该同学方案的优点是只需利用刻度尺测量A位置到桌面的高度h,桌面到地面的高度H及平抛运动的水平位移L即可.
(1)用游标卡尺测出小球的直径d如图(b)所示,d=1.140cm;
(2)为了测量小球下降的高度,若不测小球的直径d,则从位置A中球的下边沿(填“球的下边沿”或“球心”)到桌面的距离即为小球下降的高度h;
(3)实验中改变h,多测几次h和L的数值,作出如图(c)所示的图象1,则该图象的斜率k=4H可证明小球下摆过程中机械能守恒;
(4)若作出的图象为如图(c)所示的图象2,原因是h测大了.
分析 解决本题的关键掌握游标卡尺读数的方法,主尺读数加上游标读数,不需估读.
根据球先做圆周运动,再做平抛运动,结合平抛处理规律,即可求解平抛的初速度,算出对应的动能,再由刻度尺量出高度,算出重力势能,进而得以验证机械能守恒,因球落地时,球下边沿与地面接触,从而可确定结果;
根据减少的重力势能转化为动能,结合纵轴表示L2,横轴表示h,即可确定图象斜率的含义;
依据图象的含义与数学表达式相结合,即可求解.
解答 解:(1)游标卡尺的主尺读数为11mm,游标尺上第8个刻度和主尺上某一刻度对齐,所以游标读数为8×0.05mm=0.40mm,所以最终读数为:11mm+0.40mm=11.40mm=1.140cm.
(2)球做平抛运动,根据水平方向匀速直线与竖直方向自由落体,对于竖直方向的高度是球下边沿离开桌面,到下落到地面,因此测量A位置到桌面的高度h应从球下边沿开始测量;
(3)根据球做平抛运动,则有:L=v$\sqrt{\frac{2H}{g}}$
而球做圆周运动时,则有:mgh=$\frac{1}{2}$mv2,
联立上两式,解得:L2=4Hh
因此该同学取纵轴表示L2,则横轴应表示h,那么图象的斜率k=4H,
(4)若作出的图象为如图(c)所示的图象2,依据数学表达式,纵截距不为零,造成原因是h测大了.
故答案为:(1)1.140;(2)球的下边沿;(3)4H;(4)h测大了.
点评 考查如何验证机械能守恒定律,掌握平抛运动处理的规律,学会运动的合成与分解,注意球下落的高度从球下边沿测量是解题的关键,同时理解图象斜率的含义.

练习册系列答案
相关题目
18. 某兴趣小组自制一小型发电机,使线圈在匀强磁场中绕垂直于磁场方向的固定轴转动,穿过线圈的磁通量Φ随时间t按正弦规律变化,如图所示,线圈转动周期为T,线圈产生的电动势的最大值为Em,线圈的电阻为r,该线圈与电阻为R的纯电阻用电器构成闭合回路,则( )
某兴趣小组自制一小型发电机,使线圈在匀强磁场中绕垂直于磁场方向的固定轴转动,穿过线圈的磁通量Φ随时间t按正弦规律变化,如图所示,线圈转动周期为T,线圈产生的电动势的最大值为Em,线圈的电阻为r,该线圈与电阻为R的纯电阻用电器构成闭合回路,则( )
 某兴趣小组自制一小型发电机,使线圈在匀强磁场中绕垂直于磁场方向的固定轴转动,穿过线圈的磁通量Φ随时间t按正弦规律变化,如图所示,线圈转动周期为T,线圈产生的电动势的最大值为Em,线圈的电阻为r,该线圈与电阻为R的纯电阻用电器构成闭合回路,则( )
某兴趣小组自制一小型发电机,使线圈在匀强磁场中绕垂直于磁场方向的固定轴转动,穿过线圈的磁通量Φ随时间t按正弦规律变化,如图所示,线圈转动周期为T,线圈产生的电动势的最大值为Em,线圈的电阻为r,该线圈与电阻为R的纯电阻用电器构成闭合回路,则( )| A. | 线圈匝数为n=$\frac{T{E}_{m}}{2π{Φ}_{m}}$ | |
| B. | 电阻为R的用电器的电功率为$\frac{{{E}^{2}}_{m}}{2R}$ | |
| C. | 在0~$\frac{T}{4}$时间内通过用电器的电荷量为q=$\frac{T{E}_{m}}{2π(r+R)}$ | |
| D. | 若线圈转速增大为原来的2倍,线圈中电动势的瞬时值为e=2Emcos$\frac{2πt}{T}$ |
15. 如图所示,一根不可伸长的轻绳两端连接两轻环A.B,两环分别套在相互垂直的水平杆和竖直杆上.轻绳绕过光滑的轻小滑轮,重物悬挂于滑轮下,始终处于静止状态.下列说法正确的是( )
如图所示,一根不可伸长的轻绳两端连接两轻环A.B,两环分别套在相互垂直的水平杆和竖直杆上.轻绳绕过光滑的轻小滑轮,重物悬挂于滑轮下,始终处于静止状态.下列说法正确的是( )
 如图所示,一根不可伸长的轻绳两端连接两轻环A.B,两环分别套在相互垂直的水平杆和竖直杆上.轻绳绕过光滑的轻小滑轮,重物悬挂于滑轮下,始终处于静止状态.下列说法正确的是( )
如图所示,一根不可伸长的轻绳两端连接两轻环A.B,两环分别套在相互垂直的水平杆和竖直杆上.轻绳绕过光滑的轻小滑轮,重物悬挂于滑轮下,始终处于静止状态.下列说法正确的是( )| A. | 只将环A向下移动少许,绳上拉力不变,环B所受摩擦力不变 | |
| B. | 只将环A向下移动少许,绳上拉力变大,环B所受摩擦力变小 | |
| C. | 只将环B向右移动少许,绳上拉力变大,环A所受杆的弹力不变 | |
| D. | 只将环B向右移动少许,绳上拉力不变,环A所受杆的弹力变小 |
 如图所示,一侧带有光滑弧面的劈A和物体B静止在光滑水平面上,劈的底端与地面相切,物体B左端固定一轻质弹簧,小球C从劈A上距离水平高度为h处沿光滑的弧面滑下,然后滑到物体B处挤压弹簧,已知劈A、物体B、小球C质量均为m,重力加速度为g,求:
如图所示,一侧带有光滑弧面的劈A和物体B静止在光滑水平面上,劈的底端与地面相切,物体B左端固定一轻质弹簧,小球C从劈A上距离水平高度为h处沿光滑的弧面滑下,然后滑到物体B处挤压弹簧,已知劈A、物体B、小球C质量均为m,重力加速度为g,求: 如图所示,一由两种材料制成的直角三棱镜上部为材料一,下部为材料二,图中MN为分界面,两束相同的单色光a、b垂直于棱镜AB边射入,a光束在AC面上刚好发生全反射,已知棱镜的顶角∠A=45°,则棱镜对此单色光的折射率为$\sqrt{2}$,b光在AC面上发生了反射和折射,折射光线与AC面的夹角为30°,则该材料二的折射率为$\frac{\sqrt{6}}{2}$.
如图所示,一由两种材料制成的直角三棱镜上部为材料一,下部为材料二,图中MN为分界面,两束相同的单色光a、b垂直于棱镜AB边射入,a光束在AC面上刚好发生全反射,已知棱镜的顶角∠A=45°,则棱镜对此单色光的折射率为$\sqrt{2}$,b光在AC面上发生了反射和折射,折射光线与AC面的夹角为30°,则该材料二的折射率为$\frac{\sqrt{6}}{2}$.

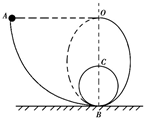 如图所示,光滑轨道ABCBO在同一竖直平面内,AB段为半径为R的四分之一圆弧,圆心在O点,该圆弧与圆轨道BCB及半椭圆形轨道BO相切于B点,现让一质量为m的小球以向下的初速度v0从A点进入轨道,结果在C点对圆轨道的压力为F,在O点对轨道的压力恰好为零.
如图所示,光滑轨道ABCBO在同一竖直平面内,AB段为半径为R的四分之一圆弧,圆心在O点,该圆弧与圆轨道BCB及半椭圆形轨道BO相切于B点,现让一质量为m的小球以向下的初速度v0从A点进入轨道,结果在C点对圆轨道的压力为F,在O点对轨道的压力恰好为零.