题目内容
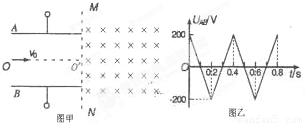 (选做).如图甲所示,两平行金属板间接有如图乙所示的随时间t变化的电压UAB,两板间电场可看做是均匀的,且两板外无电场,极板长L=0.2m,板间距离d=0.2m,在金属板右侧有一边界为MN的区域足够大的匀强磁场,MN与两板间中线OO′垂直,磁感应强度B=5×l0-3T,方向垂直纸面向里.现有带正电的粒子流沿两板中线OO′连续射入电场中,已知每个粒子的速度v=105m/s,比荷
(选做).如图甲所示,两平行金属板间接有如图乙所示的随时间t变化的电压UAB,两板间电场可看做是均匀的,且两板外无电场,极板长L=0.2m,板间距离d=0.2m,在金属板右侧有一边界为MN的区域足够大的匀强磁场,MN与两板间中线OO′垂直,磁感应强度B=5×l0-3T,方向垂直纸面向里.现有带正电的粒子流沿两板中线OO′连续射入电场中,已知每个粒子的速度v=105m/s,比荷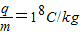 ,重力忽略不计,每个粒子通过电场区域的时间极短,此极短时间内电场可视作是恒定不变的.求:
,重力忽略不计,每个粒子通过电场区域的时间极短,此极短时间内电场可视作是恒定不变的.求:(1)在t=0.ls时刻射入电场的带电粒子,进入磁场时在MN上的入射点和出磁场时在MN上的出射点间的距离为多少;
(2)带电粒子射出电场时的最大速度;
(3)在t=0.25s时刻从电场射出的带电粒子,在磁场中运动的时间.
【答案】分析:(1)在t=0.ls时刻射入电场的带电粒子,在电场中做匀速直线运动,进入磁场做圆周运动,垂直边界进入磁场,知运动半个圆周射出,在MN上射入点和射出点的距离为2R.
(2)带电粒子从极板的边缘射出电场时速度最大,根据带电粒子在磁场中做类平抛运动,根据沿电场方向上的匀加速直线运动,求出偏转的电压,根据动能定律求出射出电场的最大速度.
(3)在t=0.25s时偏转电压为100V,根据第二问解出的结论知,粒子贴着上边缘进入磁场,根据v=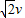 ,知垂直进入磁场时与磁场边界的夹角为
,知垂直进入磁场时与磁场边界的夹角为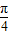 ,射出磁场时与磁场边界的夹角也为
,射出磁场时与磁场边界的夹角也为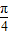 ,故对应的圆心角为
,故对应的圆心角为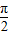 ,根据t=
,根据t=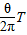 求出粒子在磁场中的运动的时间.
求出粒子在磁场中的运动的时间.
解答:解:(1)在t=0.1s时刻射入电场的带电粒子,在极板间做匀速直线运动,以v垂直磁场边界射入磁场.
由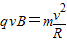 得,R=
得,R=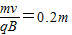
在MN上的入射点和出磁场时在MN上的出射点间的距离为d=2R=0.4m.
(2)设带电粒子从极板的边缘射出电场时速度最大,对应的瞬时电压为u,则:
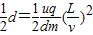 ,解得u=100V.
,解得u=100V.
由动能定理得,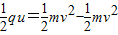 .
.
射出的最大速度v=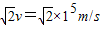 .
.
(3)在t=0.25s时刻从电场射出的带电粒子,从极板的上边缘射出电场,垂直进入磁场时与磁场边界的夹角为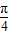 ,射出磁场时与磁场边界的夹角也为
,射出磁场时与磁场边界的夹角也为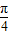 ,故对应的圆心角为
,故对应的圆心角为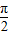 ,故在磁场中运动的时间为圆周运动周期的四分之一.
,故在磁场中运动的时间为圆周运动周期的四分之一.
由qvB=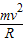 ,T=
,T=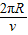 ,得T=
,得T=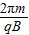 ,
,
所以t=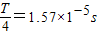 .
.
答:(1)进入磁场时在MN上的入射点和出磁场时在MN上的出射点间的距离为0.4m.
(2)带电粒子射出电场时的最大速度为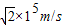 .
.
(3)在t=0.25s时刻从电场射出的带电粒子,在磁场中运动的时间为1.57×10-5s.
点评:解决本题的关键理清粒子在电场中和磁场中的运动轨迹,结合运动学公式、牛顿第二定律和动能定理进行求解.
(2)带电粒子从极板的边缘射出电场时速度最大,根据带电粒子在磁场中做类平抛运动,根据沿电场方向上的匀加速直线运动,求出偏转的电压,根据动能定律求出射出电场的最大速度.
(3)在t=0.25s时偏转电压为100V,根据第二问解出的结论知,粒子贴着上边缘进入磁场,根据v=
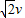 ,知垂直进入磁场时与磁场边界的夹角为
,知垂直进入磁场时与磁场边界的夹角为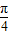 ,射出磁场时与磁场边界的夹角也为
,射出磁场时与磁场边界的夹角也为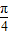 ,故对应的圆心角为
,故对应的圆心角为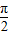 ,根据t=
,根据t=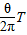 求出粒子在磁场中的运动的时间.
求出粒子在磁场中的运动的时间.解答:解:(1)在t=0.1s时刻射入电场的带电粒子,在极板间做匀速直线运动,以v垂直磁场边界射入磁场.
由
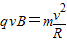 得,R=
得,R=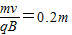
在MN上的入射点和出磁场时在MN上的出射点间的距离为d=2R=0.4m.
(2)设带电粒子从极板的边缘射出电场时速度最大,对应的瞬时电压为u,则:
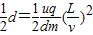 ,解得u=100V.
,解得u=100V.由动能定理得,
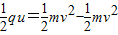 .
.射出的最大速度v=
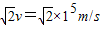 .
.(3)在t=0.25s时刻从电场射出的带电粒子,从极板的上边缘射出电场,垂直进入磁场时与磁场边界的夹角为
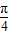 ,射出磁场时与磁场边界的夹角也为
,射出磁场时与磁场边界的夹角也为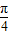 ,故对应的圆心角为
,故对应的圆心角为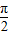 ,故在磁场中运动的时间为圆周运动周期的四分之一.
,故在磁场中运动的时间为圆周运动周期的四分之一.由qvB=
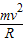 ,T=
,T=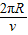 ,得T=
,得T=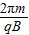 ,
,所以t=
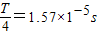 .
.答:(1)进入磁场时在MN上的入射点和出磁场时在MN上的出射点间的距离为0.4m.
(2)带电粒子射出电场时的最大速度为
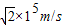 .
.(3)在t=0.25s时刻从电场射出的带电粒子,在磁场中运动的时间为1.57×10-5s.
点评:解决本题的关键理清粒子在电场中和磁场中的运动轨迹,结合运动学公式、牛顿第二定律和动能定理进行求解.

练习册系列答案
相关题目
 (2012?马鞍山模拟)(选做).如图甲所示,两平行金属板间接有如图乙所示的随时间t变化的电压UAB,两板间电场可看做是均匀的,且两板外无电场,极板长L=0.2m,板间距离d=0.2m,在金属板右侧有一边界为MN的区域足够大的匀强磁场,MN与两板间中线OO′垂直,磁感应强度B=5×l0-3T,方向垂直纸面向里.现有带正电的粒子流沿两板中线OO′连续射入电场中,已知每个粒子的速度v0=105m/s,比荷
(2012?马鞍山模拟)(选做).如图甲所示,两平行金属板间接有如图乙所示的随时间t变化的电压UAB,两板间电场可看做是均匀的,且两板外无电场,极板长L=0.2m,板间距离d=0.2m,在金属板右侧有一边界为MN的区域足够大的匀强磁场,MN与两板间中线OO′垂直,磁感应强度B=5×l0-3T,方向垂直纸面向里.现有带正电的粒子流沿两板中线OO′连续射入电场中,已知每个粒子的速度v0=105m/s,比荷
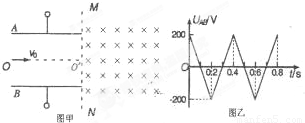 (选做).如图甲所示,两平行金属板间接有如图乙所示的随时间t变化的电压UAB,两板间电场可看做是均匀的,且两板外无电场,极板长L=0.2m,板间距离d=0.2m,在金属板右侧有一边界为MN的区域足够大的匀强磁场,MN与两板间中线OO′垂直,磁感应强度B=5×l0-3T,方向垂直纸面向里.现有带正电的粒子流沿两板中线OO′连续射入电场中,已知每个粒子的速度v=105m/s,比荷
(选做).如图甲所示,两平行金属板间接有如图乙所示的随时间t变化的电压UAB,两板间电场可看做是均匀的,且两板外无电场,极板长L=0.2m,板间距离d=0.2m,在金属板右侧有一边界为MN的区域足够大的匀强磁场,MN与两板间中线OO′垂直,磁感应强度B=5×l0-3T,方向垂直纸面向里.现有带正电的粒子流沿两板中线OO′连续射入电场中,已知每个粒子的速度v=105m/s,比荷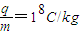 ,重力忽略不计,每个粒子通过电场区域的时间极短,此极短时间内电场可视作是恒定不变的.求:
,重力忽略不计,每个粒子通过电场区域的时间极短,此极短时间内电场可视作是恒定不变的.求: