Question

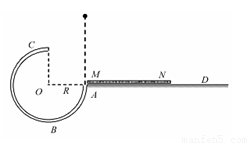
如图所示，一个3/4圆弧形光滑细圆管轨道ABC，被放置在竖直平面内，轨道半径为R，在A点与水平地面AD相接，地面与圆心O等高，MN是放在水平地面上长为3R、厚度不计的垫子，左端M正好位于A点，将一个质量为m、直径略小于圆管直径的小球从A处管口正上方某处由静止释放，不考虑空气阻力。

（1）若小球从C点射出后恰好能打到垫子的M端，则小球经过C点时对管的作用力大小和方向如何？

（2）欲使小球能通过C点落到垫子上，小球离A点的最大高度是多少？

 

Answer 1

【答案】

（1）方向竖直向下  (2) 5R

【解析】

试题分析：(1)小球离开C点做平抛运动，落到M点的水平位移为R,竖直下落的高度为R,根据运动学公式可得：，解得

从C点射出的速度为

小球在C点，根据牛顿定律 ,解得

根据牛顿第三定律，小球对管子的作用力大小为，方向竖直向下。

（2）根据机械能守恒定律，小球下落的高度越高，在C点获得的速度越大。要使小球落到垫子上，小球在水平方向的位移应该在R—4R,由于小球每次运动的时间相同，速度越大，水平方向运动的距离越大，故应使小球运动的最大位移为4R，达到N点。设能够落到N点的水平速度为v₂,根据平抛运动求得v₂=.设小球下落的最大高度为H，根据机械能守恒定律，解得。

考点：平抛运动的规律及机械能守恒定律。