Question

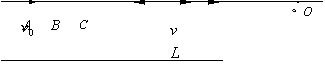
如图所示，三个半径均为r、质量均为m的小球紧靠着由静止起沿倾角为α的光滑斜面下滑，斜面与光滑水平面间有光滑小圆弧连接，开始时第一个小球的最低点离水平面的高度为h．则第三个小球滑到水平面时的速度大小v₃=

2gh+4grsinα

，在此过程中第二个小球对第一个小球所做的功W=

2mgrsinα

．

Answer 1

分析：把三个小球看成一个整体，从开始释放到水平面的过程中，运用动能定理即可求解速度，隔离第一个小球，由动能定理列式即可求解在此过程中第二个小球对第一个小球所做的功W．

解答：解：把三个小球看成一个整体，整体滑到水平面时，高度下降了H=h+2rsinα，
根据动能定理得：

1

2

?3m?v2=3mgH
解得：v=

2gh+4grsinα

隔离第一个小球，由动能定理得：
W+mgh=

1

2

mv2
解得：W=2mgrsinα，
故答案为：

2gh+4grsinα

，2mgrsinα

点评：本题主要考查了动能定理的直接应用，注意整体法和隔离法在解题时的灵活运动，难度适中．