题目内容
 如图所示,在虚线所包围的圆形区域内,有方向垂直于圆面向里的匀强磁场,从磁场边缘的A点沿半径方向射入一束速率不同的质子,这些粒子在磁场里运动的过程中,下列结论中正确的是( )
如图所示,在虚线所包围的圆形区域内,有方向垂直于圆面向里的匀强磁场,从磁场边缘的A点沿半径方向射入一束速率不同的质子,这些粒子在磁场里运动的过程中,下列结论中正确的是( )分析:设磁场区域半径为R,轨迹的圆心角为α,则粒子在磁场中运动时间为t=
T,圆心角α越大,时间越长.根据几何知识得到轨迹半径r与R的关系,就能得到轨迹长度与时间的关系.带电粒子在磁场中偏转角等于轨迹的圆心角.
| α |
| 2π |
解答: 解:设磁场区域半径为R,轨迹的圆心角为α.
解:设磁场区域半径为R,轨迹的圆心角为α.
A、粒子运动的轨迹为S=rα=Rcot
?α.粒子的运动时间越长,α越大,根据数学知识可以证明孤长S越短.故A错误.
B、粒子在磁场中运动的时间为t=
T,而轨迹半径r=Rcot
,当粒子的运动时间越短时,α越小,则知r越大,而r=
,则速度v越大.故B错误.
C、根据推论得知,带电粒子在磁场中偏转角等于轨迹的圆心角α,则在磁场中偏转越小的,轨迹的圆心角α,由t=
T知,运动时间越短.故C正确.
D、由上分析知道,速度越大,轨迹半径r越大,而tan
=
,α越小,通过磁场的时间越短.故D错误.
故选C
 解:设磁场区域半径为R,轨迹的圆心角为α.
解:设磁场区域半径为R,轨迹的圆心角为α.A、粒子运动的轨迹为S=rα=Rcot
| α |
| 2 |
B、粒子在磁场中运动的时间为t=
| α |
| 2π |
| α |
| 2 |
| mv |
| qB |
C、根据推论得知,带电粒子在磁场中偏转角等于轨迹的圆心角α,则在磁场中偏转越小的,轨迹的圆心角α,由t=
| α |
| 2π |
D、由上分析知道,速度越大,轨迹半径r越大,而tan
| α |
| 2 |
| R |
| r |
故选C
点评:本题要根据几何知识研究粒子运动的轨迹半径与磁场区域半径的关系,也可以通过作轨迹对比,得到轨迹的圆心角与运动时间、轨迹长度的关系.

练习册系列答案
相关题目
 如图所示,在虚线方框内的空间有方向竖直向下的匀强电场和垂直纸面向里的匀强磁场,一带电粒子垂直电场和磁场方向飞人场中,恰好做匀速直线运动,水平飞离正交电磁场.如果该区域只有电场,粒子将从a点飞离,穿越场区的时间为t1,飞离时速度大小为V1;如果只有磁场,粒子将从b点飞离,穿越场区的时间为t2,飞离时速度大小为V2,重力忽咯不计,则( )
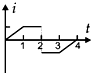
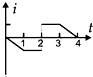
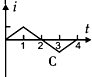
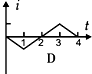
如图所示,在虚线方框内的空间有方向竖直向下的匀强电场和垂直纸面向里的匀强磁场,一带电粒子垂直电场和磁场方向飞人场中,恰好做匀速直线运动,水平飞离正交电磁场.如果该区域只有电场,粒子将从a点飞离,穿越场区的时间为t1,飞离时速度大小为V1;如果只有磁场,粒子将从b点飞离,穿越场区的时间为t2,飞离时速度大小为V2,重力忽咯不计,则( ) 如图所示,在虚线所示的等腰直角三角形CDE(其斜边DE长为3L)区域内,存在有垂直纸面向里的匀强磁场,一边长为L的正方形线框efgh(fg边与DE边在同一直线上)在纸平面内沿DE方向从左向右以速度V匀速通过场区.若以图示位置为计时起点,规定逆时针方向为线框中感应电流的正方向,则图所示的四个i-t图象(横轴单位长度表示的值为L/V),哪一个正确反映了线框中的感应电流的规律( )
如图所示,在虚线所示的等腰直角三角形CDE(其斜边DE长为3L)区域内,存在有垂直纸面向里的匀强磁场,一边长为L的正方形线框efgh(fg边与DE边在同一直线上)在纸平面内沿DE方向从左向右以速度V匀速通过场区.若以图示位置为计时起点,规定逆时针方向为线框中感应电流的正方向,则图所示的四个i-t图象(横轴单位长度表示的值为L/V),哪一个正确反映了线框中的感应电流的规律( )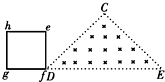 如图甲所示,在虚线所示的等腰直角三角形CDE(其底边DE长为3L)区域内,存在有垂直纸面向里的匀强磁场,一边长为L的正方形线框efgh(gf边与DE边在同一直线上)在纸平面内沿DE方向从左向右以速度v匀速通过场区.若以图示位置为计时起点,规定逆时针方向为线框中感应电流的正方向,则图乙所示的四个i-t图象(横轴单位长度表示的值为L/v),哪一个能反映线框中感应电流的规律( )
如图甲所示,在虚线所示的等腰直角三角形CDE(其底边DE长为3L)区域内,存在有垂直纸面向里的匀强磁场,一边长为L的正方形线框efgh(gf边与DE边在同一直线上)在纸平面内沿DE方向从左向右以速度v匀速通过场区.若以图示位置为计时起点,规定逆时针方向为线框中感应电流的正方向,则图乙所示的四个i-t图象(横轴单位长度表示的值为L/v),哪一个能反映线框中感应电流的规律( )