题目内容

10．如图所示，质量都为m的a、b两球固定在轻杆的两端，轻杆可绕O  点在竖直面内无摩擦转动，已知两球距O点的距离L1＞L2，在图示的水平位置由静止释放，则（　　）
A．杆对a球做正功B．杆对b球做负功C．杆对a球做负功D．杆对b球做正功

分析 a、b两球围绕同一个固定轴转动，角速度相等，根据向心加速度公式判断加速度是否相等，两小球看成一个系统，只有重力做功，系统机械能守恒，对b球进行研究可知杆对a球的做功情况．

解答 解：在a下降过程中，b球的动能增加，重力势能增加，所以b球的机械能增加，
根据重力之外的力做功量度物体机械能的变化，所以杆对b做正功，
球a和b系统机械能守恒，所以a机械能减小，所以杆对a做负功．
故A、B错误，CD正确．
故选：CD．

点评 本题是轻杆连接的模型问题，对系统机械能是守恒的，但对单个小球机械能并不守恒，运用系统机械能守恒及除重力以外的力做物体做的功等于物体机械能的变化量进行研究即可．

练习册系列答案
相关题目
20．如图甲喷出的水做斜抛运动，图乙为斜抛物体的轨迹，对轨迹上的两点A、B下列说法正确的是（不计空气阻力）（　　）
A．A点的速度方向沿切线向上，合力方向沿切线向下
B．A点的速度方向沿切线向上，合力方向竖直向下
C．B点的速度方向沿切线向下，合力方向沿切线向下
D．B点的速度方向沿切线向下，合力方向竖直向上
1．设质子、中子、氘核的质量分别为m1、m2和m3，那么，当一个质子和一个中子结合成氘核时，释放的能量是（　　）
A．m2C2B．（m1+m2）C2C．（m3-m2-m1）C2D．（m1+m2-m3）C2
18．如图所示，小球在竖直向下的力F作用下，将竖直轻弹簧压缩，若将力F撤去，小球将向上弹起并离开弹簧，直到速度为零时为止，则小球在上升过程中（　　）
A．小球的动能先减小后增大B．小球在离开弹簧时动能最大
C．小球动能最大时弹性势能为零D．小球动能减为零时，重力势能最大
5．下列关于机械振动和机械波说法正确的是（　　）
A．简谐波一定是横波，波上的质点均做简谐运动
B．两个完全相同的振源产生的波相遇时，振动振幅最大的质点是发生了共振
C．在平直公路上一辆警车鸣着笛匀速驶过一站在路边的观察者，警车发出的笛声频率恒定，观察者听到的笛声频率先逐渐变小，后逐渐变大
D．可闻声波比超声波更容易发生明显的衍射，是因为可闻声波的波长比超声波的波长更长
15．假设地球可视为质量均匀分布的球体，己知地球表面重力加速度在两极的大小为g0，在赤道处的大小为g，地球自转的周期为T．则地球的半径为（　　）
A．$\frac{（{g}_{0}-g）{T}^{2}}{4{π}^{2}}$B．$\frac{4{π}^{2}}{（{g}_{0}-g）{T}^{2}}$C．$\frac{（{g}_{0}+g）{T}^{2}}{4{π}^{2}}$D．$\frac{4{π}^{2}}{（{g}_{0}+g）{T}^{2}}$
2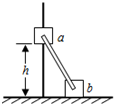．如图所示，滑块a、b的质量均为m，a套在固定光滑竖直杆上，与光滑水平地面相距h，b放在地面上，a、b通过铰链用刚性轻杆连接，不计摩擦，a、b可视为质点，重力加速度大小为g．下列判断正确的是（　　）
A．a下落的某段过程中，b对地面的压力可能大于b受到地面的支持力
B．a落地前，轻杆对b先做正功后做负功
C．a下落的某段过程中，其加速度大小可能大于g
D．a落地前瞬间a的机械能最小，此时b对地面的压力大小等于mg
19．请用学过的运动和力的知识判断下列说法正确的是（　　）
A．描述一个物体的运动时，参考系可以任意选择．选择不同的参考系来观察同一个物体的运动，其结果可能会有所不同
B．重的物体比轻的物体下落的快，是因为重的物体受到的重力大，加速度大
C．子弹的质量并不重，之所以能对人造成伤害是因为其高速运动时的惯性很大
D．既然作用力和反作用力是大小相等、方向相反的，他们应该互相平衡
20．有一质量为m的小木块，由碗边滑向碗底，碗的内表面是半径为R的圆弧，由于摩擦力的作用，木块运动的速率不变，则木块（　　）
A．对碗的压力大小不变B．对碗的压力始终大于重力
C．运动的加速度恒定D．所受合外力大小不变

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网