题目内容
16. 如图所示,让摆球从图中的C位置由静止开始摆下,摆到最低点D处,摆线刚好被拉断,小球在粗糙的水平面上由D点向右做匀减速运动,到达小A孔进入半径R=0.3m的竖直放置的光滑圆弧轨道,当摆球进入圆轨道立即关闭A孔.已知摆线长L=2m,θ=60°,小球质量为m=1kg,D点与小孔A的水平距离s=2m,g取10m/s2.试求:
如图所示,让摆球从图中的C位置由静止开始摆下,摆到最低点D处,摆线刚好被拉断,小球在粗糙的水平面上由D点向右做匀减速运动,到达小A孔进入半径R=0.3m的竖直放置的光滑圆弧轨道,当摆球进入圆轨道立即关闭A孔.已知摆线长L=2m,θ=60°,小球质量为m=1kg,D点与小孔A的水平距离s=2m,g取10m/s2.试求:(1)求摆线能承受的最大拉力为多大?
(2)要使摆球能进入圆轨道并且不脱离轨道,求粗糙水平面摩擦因数μ的范围.
分析 (1)摆球摆到D点时,摆线的拉力最大,根据机械能守恒定律求出摆球摆到D点时速度,由牛顿第二定律求出摆线的最大拉力.
(2)要使摆球能进入圆轨道,并且不脱离轨道,有两种情况:一种在圆心以下做等幅摆动;另一种能通过圆轨道做完整的圆周运动.
小球要刚好运动到A点,对小球从D到A的过程,运用动能定理求出动摩擦因数μ的最大值;
若小球进入A孔的速度较小,并且不脱离轨道,那么将会在圆心以下做等幅摆动,不脱离轨道,其临界情况为到达圆心等高处速度为零,根据机械能守恒和动能定理求出动摩擦因数.
要使摆球能进入圆轨道,恰好到达轨道的最高点,就刚好不脱离轨道,在最高点时,由重力提供向心力,由牛顿第二定律求出此时小球的速度,对从D到轨道最高点的过程,运用动能定理求解动摩擦因数的最小值,即可得到μ的范围.
解答 解:(1)当摆球由C到D运动,机械能守恒,则得:mg(L-Lcosθ)=$\frac{1}{2}m{{v}_{D}}^{2}$,
在D点,由牛顿第二定律可得:Fm-mg=$m\frac{{{v}_{D}}^{2}}{L}$,
代入数据解得Fm=20N.
(2)小球不脱圆轨道分两种情况:
①要保证小球能达到A孔,设小球到达A孔的速度恰好为零,
对小球从D到A的过程,由动能定理可得:-μ1mgs=0-$\frac{1}{2}m{{v}_{D}}^{2}$
解得:μ1=0.5
若进入A孔的速度较小,那么将会在圆心以下做等幅摆动,不脱离轨道.其临界情况为到达圆心等高处速度为零,由机械能守恒可得:$\frac{1}{2}m{{v}_{A}}^{2}=mgR$,
由动能定理可得:-μ2mgs=$\frac{1}{2}m{{v}_{A}}^{2}-\frac{1}{2}m{{v}_{D}}^{2}$,
解得:μ2=0.35
②若小球能过圆轨道的最高点则不会脱离轨道,在圆周的最高点由牛顿第二定律可得:$mg=m\frac{{v}^{2}}{R}$,
由动能定理可得:$-{μ}_{3}mgs-2mgR=\frac{1}{2}m{v}^{2}-\frac{1}{2}m{{v}_{D}}^{2}$,
解得:μ3=0.125
综上,所以摩擦因数μ的范围为:0.35≤μ≤0.5或者μ≤0.125
答:(1)摆线能承受的最大拉力为20N;
(2)粗糙水平面摩擦因数μ的范围为:0.35≤μ≤0.5或者μ≤0.125.
点评 本题关键是不能漏解,要知道摆球能进入圆轨道不脱离轨道,有两种情况,再根据牛顿第二定律、机械能守恒和动能定理结合进行求解.

 如图甲所示,在列车首节车厢下面安装一电磁铁,电磁铁产生垂直于地面的匀强磁场,首节车厢经过安放在两铁轨间的线圈时,线圈产生的电脉冲信号传到控制中心.图乙为某时控制中心显示屏上的电脉冲信号,则此时列车的运动情况是( )
如图甲所示,在列车首节车厢下面安装一电磁铁,电磁铁产生垂直于地面的匀强磁场,首节车厢经过安放在两铁轨间的线圈时,线圈产生的电脉冲信号传到控制中心.图乙为某时控制中心显示屏上的电脉冲信号,则此时列车的运动情况是( )| A. | 匀速运动 | B. | 匀加速运动 | C. | 匀减速运动 | D. | 变加速运动 |
 “电子能量分析器”主要由处于真空中的电子偏转器和探测板组成.偏转器是由两个相互绝缘、半径分别为RA和RB的同心金属半球面A和B构成,A、B为电势值不等的等势面电势分别为φA和φB,其过球心的截面如图所示.一束电荷量为e、质量为m的电子以不同的动能从偏转器左端M的正中间小孔垂直入射,进入偏转电场区域,最后到达偏转器右端的探测板N,其中动能为Ek0的电子沿等势面C做匀速圆周运动到达N板的正中间.忽略电场的边缘效应.下列说法中正确的是( )
“电子能量分析器”主要由处于真空中的电子偏转器和探测板组成.偏转器是由两个相互绝缘、半径分别为RA和RB的同心金属半球面A和B构成,A、B为电势值不等的等势面电势分别为φA和φB,其过球心的截面如图所示.一束电荷量为e、质量为m的电子以不同的动能从偏转器左端M的正中间小孔垂直入射,进入偏转电场区域,最后到达偏转器右端的探测板N,其中动能为Ek0的电子沿等势面C做匀速圆周运动到达N板的正中间.忽略电场的边缘效应.下列说法中正确的是( )| A. | A球面电势比B球面电势低 | |
| B. | 电子在AB间偏转电场中做匀变速运动 | |
| C. | 等势面C所在处电场强度的大小为E=$\frac{{4{E_{k0}}}}{{e({{R_A}+{R_B}})}}$ | |
| D. | 等势面C所在处电势大小为$\frac{{{φ_A}+{φ_B}}}{2}$ |
 如图所示,一个长为L,质量为M的长方形木板,静止在光滑水平面上,一个质量为m的物块(可视为质点),以水平初速度v0,从木板的左端滑向另一端,设物块与木板间的动摩擦因数为μ,当物块与木板达到相对静止时,物块仍在长木板上,物块相对木板的位移为d,木板相对地面的位移为s.则在此过程中( )
如图所示,一个长为L,质量为M的长方形木板,静止在光滑水平面上,一个质量为m的物块(可视为质点),以水平初速度v0,从木板的左端滑向另一端,设物块与木板间的动摩擦因数为μ,当物块与木板达到相对静止时,物块仍在长木板上,物块相对木板的位移为d,木板相对地面的位移为s.则在此过程中( )| A. | 摩擦力对物块做功为-μmg(s+d) | |
| B. | 摩擦力对木板做功为-μmgs | |
| C. | 木板动能的增量为 μmgs | |
| D. | 系统由于摩擦而产生的热量为 μmgd |
 如图所示,放在水平桌面上的质量为1kg的物体A通过水平轻绳、轻弹簧和光滑定滑轮与物体B相连接,两物体均静止时弹簧秤甲和乙的读数分别为5N和2N,则剪断物体A左侧轻绳瞬间,物体A的加速度和弹簧秤乙的读数分别为( )
如图所示,放在水平桌面上的质量为1kg的物体A通过水平轻绳、轻弹簧和光滑定滑轮与物体B相连接,两物体均静止时弹簧秤甲和乙的读数分别为5N和2N,则剪断物体A左侧轻绳瞬间,物体A的加速度和弹簧秤乙的读数分别为( )| A. | 5 m/s2,0 | B. | 2 m/s2,2 N | C. | 0,0 | D. | 0,2 N |
 如图所示,坐标原点处有一波源,起振方向为y轴负方向,形成的一列简谐横波沿x轴正方向传播.从波传到x=1m的P点时开始计时,已知在t=0.4s时PM间第一次形成如图所示的波形,此时x=4m的M点正好在波谷.下列说法中正确的是( )
如图所示,坐标原点处有一波源,起振方向为y轴负方向,形成的一列简谐横波沿x轴正方向传播.从波传到x=1m的P点时开始计时,已知在t=0.4s时PM间第一次形成如图所示的波形,此时x=4m的M点正好在波谷.下列说法中正确的是( )| A. | P点的振动周期为0.4s | B. | P点开始振动的方向沿y轴正方向 | ||
| C. | 当M点开始振动时,P点正好在波谷 | D. | 这列波的传播速度是10m/s |
 某同学用如图1所示的电路测量欧姆表的内阻和电源电动势(把欧姆表看成一个电源,且已选定倍率并进行了欧姆调零).实验器材的规格如下:
某同学用如图1所示的电路测量欧姆表的内阻和电源电动势(把欧姆表看成一个电源,且已选定倍率并进行了欧姆调零).实验器材的规格如下:电流表A1(量程200 μA,内阻R1=300Ω)
电流表A2(量程30mA,内阻R2=5Ω)
定值电阻R0=9 700Ω
滑动变阻器R(阻值范围0~500Ω)
(1)闭合开关S,移动滑动变阻器的滑动触头至某一位置,读出电流表A1和A2的示数分别为I1和I2.多次改变滑动触头的位置,得到的数据见表.
| I1(μA) | 120 | 125 | 130 | 135 | 140 | 145 |
| I2(mA) | 20.0 | 16.7 | 13.2 | 10.0 | 6.7 | 3.3 |
(2)将该欧姆表两个表笔短接时,通过欧姆表的电流为0.10A
(3)若某次电流表A1的示数是114 μA,则此时欧姆表示数约为47.5Ω (结果保留3位有效数字)
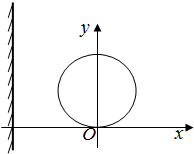 如图所示,x轴正方向水平向右,y轴正方向竖直向上.在xoy平面内有与y轴平行的匀强电场,在圆心为C半径为R的圆内还有与xoy平面垂直的匀强磁场.在原点O放置一带电微粒发射装置,它发射出质量为m、电荷量为q(q>0)和初速度大小为v的同种带电微粒,速度方向分布在xoy平面第一和第二象限内的各个方向上.已知从O点沿y轴正方向发射的带电微粒射出磁场区域后平行于x轴运动.在x轴上有一与y轴平行的荧光屏.重力加速度为g.
如图所示,x轴正方向水平向右,y轴正方向竖直向上.在xoy平面内有与y轴平行的匀强电场,在圆心为C半径为R的圆内还有与xoy平面垂直的匀强磁场.在原点O放置一带电微粒发射装置,它发射出质量为m、电荷量为q(q>0)和初速度大小为v的同种带电微粒,速度方向分布在xoy平面第一和第二象限内的各个方向上.已知从O点沿y轴正方向发射的带电微粒射出磁场区域后平行于x轴运动.在x轴上有一与y轴平行的荧光屏.重力加速度为g. 如图所示的皮带传动装置,主动轮1的半径与从动轮2的半径之比R1:R2=5:2,A、B分别是两轮边缘上的点,假设皮带不打滑,则
如图所示的皮带传动装置,主动轮1的半径与从动轮2的半径之比R1:R2=5:2,A、B分别是两轮边缘上的点,假设皮带不打滑,则