题目内容
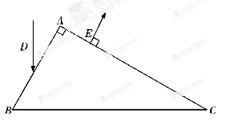
水平放置的三棱镜截面如图所示,∠A=90°,∠B=60°,AB=10cm.一束竖直向下的光束从AB边中点D入射,折射光经过三棱镜BC边反射后,从AC边上的E点垂直射出.已知真空中的光速C=3x 108m/s,求:①三棱镜的折射率;
②光在三棱镜中从D到E所用的时间.

【答案】分析:①作出光路图,根据几何知识求出光线通过AB面时的入射角i和折射角r,由光的折射定律n=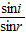 求解折射率.
求解折射率.
②光在三棱镜中速度为v=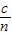 ,由几何知识求出光在三棱镜中通过的路程s,由t=
,由几何知识求出光在三棱镜中通过的路程s,由t=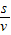 求出光在三棱镜中从D到E所用的时间.
求出光在三棱镜中从D到E所用的时间.
解答: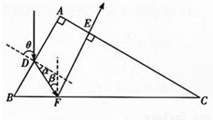 解:①作出光路图如图所示,根据几何知识得:θ=∠B=60°,α=β=30°.
解:①作出光路图如图所示,根据几何知识得:θ=∠B=60°,α=β=30°.
由折射定律得三棱镜的折射率为:n=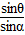 =
=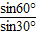 =
=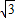
②光在三棱镜中速度为:v=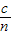 ,
,
由几何关系得: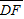 =
=
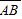 =5cm
=5cm
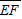 =(
=(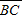 -
-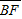 )sin30°=7.5cm
)sin30°=7.5cm
故光在三棱镜中从D到E所用的时间为:t=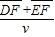 =
=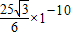 s
s
答:①三棱镜的折射率为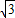 ;
;
②光在三棱镜中从D到E所用的时间为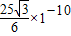 s.
s.
点评:本题是几何光学问题,作出光路图是解题的关键之处,再运用几何知识求出入射角、折射角和光程,即能很容易解决此类问题.
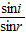 求解折射率.
求解折射率.②光在三棱镜中速度为v=
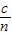 ,由几何知识求出光在三棱镜中通过的路程s,由t=
,由几何知识求出光在三棱镜中通过的路程s,由t=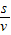 求出光在三棱镜中从D到E所用的时间.
求出光在三棱镜中从D到E所用的时间.解答:
 解:①作出光路图如图所示,根据几何知识得:θ=∠B=60°,α=β=30°.
解:①作出光路图如图所示,根据几何知识得:θ=∠B=60°,α=β=30°.由折射定律得三棱镜的折射率为:n=
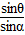 =
=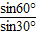 =
=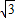
②光在三棱镜中速度为:v=
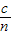 ,
,由几何关系得:
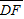 =
=
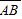 =5cm
=5cm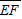 =(
=(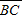 -
-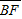 )sin30°=7.5cm
)sin30°=7.5cm故光在三棱镜中从D到E所用的时间为:t=
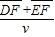 =
=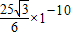 s
s答:①三棱镜的折射率为
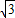 ;
; ②光在三棱镜中从D到E所用的时间为
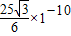 s.
s.点评:本题是几何光学问题,作出光路图是解题的关键之处,再运用几何知识求出入射角、折射角和光程,即能很容易解决此类问题.

练习册系列答案
相关题目
 水平放置的三棱镜截面如图所示,∠A=90°,∠B=60°,AB=10cm.一束竖直向下的光束从AB边中点D入射,折射光经过三棱镜BC边反射后,从AC边上的E点垂直射出.已知真空中的光速C=3x 108m/s,求:
水平放置的三棱镜截面如图所示,∠A=90°,∠B=60°,AB=10cm.一束竖直向下的光束从AB边中点D入射,折射光经过三棱镜BC边反射后,从AC边上的E点垂直射出.已知真空中的光速C=3x 108m/s,求: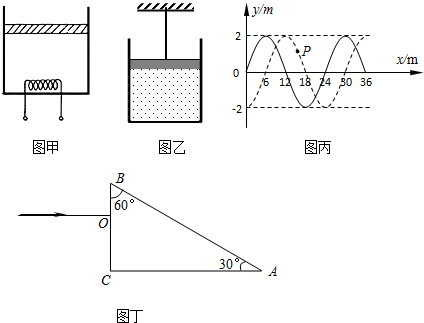

 列波的波速.
列波的波速.