题目内容
如图所示，一根跨越一固定的水平光滑细杆的轻绳，两端各系一个小球．球a置于地面，球b被拉到与细杆同一水平的位置．在绳刚拉直时放手，使球b从静止状态向下摆动．当摆到Ob段轻绳与竖直方向的夹角为60°时，球a刚要离地，求球a质量与球b质量之比．（已知图中Ob段的长度小于Oa段的长度）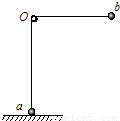
【答案】分析：当b球摆到Ob段轻绳与竖直方向的夹角为60°时，a球刚要离开地面．则绳子的拉力大小等于a球的重力．由牛顿第二定律，结合向心力公式可列出质量、速度及半径间的关系；再运用动能定理即可求解．
解答：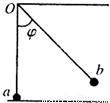
解：在a球离地前，释放后的b球一直以ob绳长L为半径在竖直平面内做圆周运动，设b球下摆至任一位置时，速度为v，摆线与铅直方向成?角，如图所示．
B球在下摆过程中，绳的拉力T不做功，故系统机械能守恒，选取悬点O所在高度为重力势能零点，设Ob的长度为L，令球a的质量为m1，球b的质量为m2，
根据动能定理有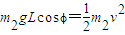
①
随着?角的减小，v及T逐渐增大，当T=m1g时，a球刚好离地，
对b球于是有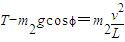
②
由①②式解得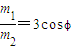
代入已知数据，得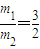
答：球a质量与球b质量之比为3：2
点评：小球b在下摆过程中运用机械能守恒定律，在最低点运用牛顿第二定律．同时借助于小球a 的重力得知小球b摆到Ob段轻绳与竖直方向的夹角为60°时绳子的拉力大小，从而将两球质量联系起来．
解答：
解：在a球离地前，释放后的b球一直以ob绳长L为半径在竖直平面内做圆周运动，设b球下摆至任一位置时，速度为v，摆线与铅直方向成?角，如图所示．B球在下摆过程中，绳的拉力T不做功，故系统机械能守恒，选取悬点O所在高度为重力势能零点，设Ob的长度为L，令球a的质量为m1，球b的质量为m2，
根据动能定理有
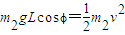①随着?角的减小，v及T逐渐增大，当T=m1g时，a球刚好离地，
对b球于是有
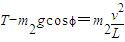②由①②式解得
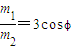
代入已知数据，得
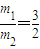
答：球a质量与球b质量之比为3：2
点评：小球b在下摆过程中运用机械能守恒定律，在最低点运用牛顿第二定律．同时借助于小球a 的重力得知小球b摆到Ob段轻绳与竖直方向的夹角为60°时绳子的拉力大小，从而将两球质量联系起来．
练习册系列答案
相关题目
如图所示，一根跨越一固定的水平光滑细杆、轻绳两端拴有两个质量均为m的小球a和b（可视为质点），Oa段的长度为L1，Ob段的长度为L2，且L1＞L2，球a置于地面，球b被拉到与细杆水平的位置，在绳刚拉直时放手，小球b从静止状态向下摆动，当球b摆到最低点时，恰好与球a在同一水平位置发生碰撞并粘合在一起，设碰撞时间极短，往后两球以O点为圆心做圆周运动，若已知碰前瞬间球a的速度大小为va，方向竖直向上，轻绳不可伸长且始终处于绷紧状态，求：
如图所示，一根跨越一固定的水平光滑细杆的轻绳，两端各系一个小球，球a置放于地面，球b被拉到与细杆同一水平的位置，在绳刚被拉直时放手，使球b从静止状态向下摆动．设两球质量相等，则球a刚要离开地面时，跨越细杆的两段绳之问的夹角为（ ）
（2004?南京三模）如图所示，一根跨越一固定的水平光滑细杆的轻绳，两端各系一个小球．球a置于地面，球b被拉到与细杆同一水平的位置．在绳刚拉直时放手，使球b从静止状态向下摆动．当摆到Ob段轻绳与竖直方向的夹角为60°时，球a刚要离地，求球a质量与球b质量之比．（已知图中Ob段的长度小于Oa段的长度）
