题目内容
14．
质量为m、长为L的导体棒MN电阻为R，起初静止于光滑的水平轨道上，电源电动势为E，内阻不计，匀强磁场的磁感应强度为B，其方向与轨道平面成θ角斜向右上方，求开关闭合瞬间导体棒的加速度．
分析 根据左手定则来确定通电导线的安培力的方向，闭合电路欧姆定律与安培力公式结合可求出其力的大小，最后由牛顿第二定律来确定导体棒瞬间的加速度
解答 解：由闭合电路欧姆定律可知，I=$\frac{E}{R}$；
根据安培力公式：F=BIL
解得：F=$\frac{BLE}{R}$
根据受力分析可知，物体受到的合外力为Fsinα；
根据牛顿第二定律可得：
Fsinα=ma
解得：a=$\frac{BELsinθ}{m}$
答：开关闭合瞬间导体棒的加速度为$\frac{BELsinθ}{m}$．
点评 本题考查了闭合电路欧姆定律、牛顿第二定律、安培力的大小公式及力的分解，注意左手定则与右手定则的区别．同时注意安培力的方向与导轨的夹角．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
4．将力F分解成F1和F2，若已知F1的大小和F2与F的夹角θ（锐角），则下列说法错误的是（ ）
| A． | 当F＞F1＞Fsinθ时，有两解 | B． | 当F1=Fsinθ时，有唯一解 | ||
| C． | 当Fsinθ＜F1＜F时，有三解 | D． | 当F1＜Fsinθ时，无解 |
2．如图所示为一矩形磁场区域abcd，ab、cd两边足够长，ad边长为d，矩形区域内有一垂直纸面向外的匀强磁场，磁感应强度为B．在ad边的中点P放一粒子源，若该离子源可在纸面内向各个方向发射电荷量为q、质量为m、速度为v=$\frac{qBd}{m}$的正粒子，粒子的重力不计．则粒子打在cd边上的长度为多少？（ ）
| A． | $（\frac{{\sqrt{3}}}{2}+1）d$ | B． | $\frac{{\sqrt{17}}}{2}d$ | C． | d | D． | $\frac{{\sqrt{3}}}{2}d$ |
如图所示，坐标系xOy在竖直平面内，x轴沿水平方向，x＞0的区域有垂直坐标平面向外的匀强磁场，磁感应强度大小为B1；第三象限内存在垂直坐标平面向外、磁感应强度大小为B2的匀强磁场和竖直向上、电场强度大小为E的匀强电场；x＞0的区域固定一与x轴成θ=30°角的绝缘细杆，一个穿在细杆上的带电小球a沿细杆匀速下滑，从N点恰能沿圆周轨道运动到x轴上的Q点，且速度方向垂直x轴．已知Q点到坐标原点O的距离为L，B1=$\frac{7E}{2}$$\sqrt{\frac{3}{5πgL}}$，B2=$\frac{E}{2}$$\sqrt{\frac{5π}{gL}}$，重力加速度为g，不计空气阻力．
某实验小组选择了日常生活中使用的电子秤、保温水壶、细线、墙钉和白纸等物品，做“验证力的平行四边形定则”的实验．他们将水壶装上适量的水，如图甲所示，将三根细线L1、L2、L3的一端打结，另一端分别拴在电子秤的挂钩、墙钉A和水壶带子上．
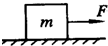如图所示，质量m=10kg的物体放在水平面上，物体与水平面间动摩擦因数为μ=0.4，取g=10m/s2，今用大小为F=50N的水平恒力作用于物体，使物体由静止开始做匀变速直线运动，经t=8s，求：