题目内容
3. 如图所示,长为L的细绳上端系一质量不计的环,环套在光滑水平杆上,在细绳的下端吊一个质量为m的铁球(可视作质点),球离地的高度h=L,当绳受到大小为2.8mg的拉力时就会断裂,现让环与球一起以v=$\sqrt{2gL}$的速度向右匀速运动,在A处环被挡住而立即停止,已知A离右墙的水平距离也为L,当地的重力加速度为g,不计空气阻力.
如图所示,长为L的细绳上端系一质量不计的环,环套在光滑水平杆上,在细绳的下端吊一个质量为m的铁球(可视作质点),球离地的高度h=L,当绳受到大小为2.8mg的拉力时就会断裂,现让环与球一起以v=$\sqrt{2gL}$的速度向右匀速运动,在A处环被挡住而立即停止,已知A离右墙的水平距离也为L,当地的重力加速度为g,不计空气阻力.(1)试通过计算分析环在被挡住停止运动时绳子是否会断;
(2)球的第一次碰撞点离墙角B点的距离是多少.
分析 (1)在环由运动到被挡住而立即停止后,小球立即以速率v绕A点做圆周运动,由重力与绳子的拉力的合力提供向心力,根据牛顿第二定律求出绳子的拉力,即可判断绳子不否会断.
(2)绳断裂后小球做平抛运动,利用平抛运动的规律列式求解即可.
解答 解:(1)在环被挡住而立即停止后小球立即以速率v绕A点做圆周运动,假设绳子不断,拉力为F.
根据牛顿第二定律有:
F-mg=m$\frac{{v}^{2}}{L}$
解得绳对小球的拉力大小为:F=3mg>2.8mg
所以绳子会断.
(2)绳子断裂后小球做平抛运动.
假设小球直接落到地面上,则:h=L=$\frac{1}{2}$gt2.
球的水平位移:x=vt=2L>L
所以小球先与右边的墙壁碰撞后再落到地面上
设球平抛运动到右墙的时间为t′,则t′=$\frac{L}{v}$=$\frac{L}{\sqrt{2gL}}$=$\sqrt{\frac{L}{2g}}$
小球下落的高度 h′=$\frac{1}{2}$gt′2=$\frac{L}{4}$
所以球的第一次碰撞点距B的距离为:H=L-$\frac{L}{4}$=$\frac{3}{4}$L
答:
(1)绳子会断.
(2)球的第一次碰撞点离墙角B点的距离是$\frac{3}{4}$L.
点评 本题是圆周运动与平抛运动的综合,运用假设法判断小球能否与墙碰撞.小球与墙碰撞过程,与光的反射相似,具有对称性.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
14.如图甲所示,甲为一台小型发电机构造示意图,线圈逆时针转动,产生的电动势随时间变化的正弦规律如图乙所示.发电机线圈内阻为1Ω,外接灯泡的电阻为9Ω恒定不变,则下列说法中正确的为( ) 

| A. | 电压表的示数为6V | |
| B. | 通过电阻的电流方向1秒钟改变50次 | |
| C. | 在0.01s时刻,穿过线圈的磁通量最大 | |
| D. | 产生该交变电流的线圈在磁场中匀速转动的角速度为50π rad/s |
11.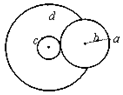 如图所示的靠轮传动(静摩擦力传动)装置中右轮半径为2r,a为它边缘上的一点,b为轮上的一点,b距轴为r.左侧为一轮轴(大小轮同步转动),大轮的半径为4r,d为它边缘上的一点,小轮的半径为r,c为它边缘上的一点.若传动中靠轮不打滑,则下列说法错误的是( )
如图所示的靠轮传动(静摩擦力传动)装置中右轮半径为2r,a为它边缘上的一点,b为轮上的一点,b距轴为r.左侧为一轮轴(大小轮同步转动),大轮的半径为4r,d为它边缘上的一点,小轮的半径为r,c为它边缘上的一点.若传动中靠轮不打滑,则下列说法错误的是( )
 如图所示的靠轮传动(静摩擦力传动)装置中右轮半径为2r,a为它边缘上的一点,b为轮上的一点,b距轴为r.左侧为一轮轴(大小轮同步转动),大轮的半径为4r,d为它边缘上的一点,小轮的半径为r,c为它边缘上的一点.若传动中靠轮不打滑,则下列说法错误的是( )
如图所示的靠轮传动(静摩擦力传动)装置中右轮半径为2r,a为它边缘上的一点,b为轮上的一点,b距轴为r.左侧为一轮轴(大小轮同步转动),大轮的半径为4r,d为它边缘上的一点,小轮的半径为r,c为它边缘上的一点.若传动中靠轮不打滑,则下列说法错误的是( )| A. | b点与d点的线速度大小相等 | |
| B. | a点与c点的线速度大小相等 | |
| C. | c点与b点的角速度大小不相等 | |
| D. | a点与d点的向心加速度大小之比为1:8 |
18.关于匀速圆周运动中的向心加速度说法不正确的是( )
| A. | 向心加速度方向不变,总是指向圆心 | |
| B. | 向心加速度大小保持不变 | |
| C. | 向心加速度可以用线速度和半径表示 | |
| D. | 是表征线速度方向变化快慢的物理量 |
15. 当转台匀速转动时,用同种材料制成的a、b、c三个物体都相对于转台静止不动,如图所示.若ma=2mb=2mc,rc=2ra=2rb,则下列说法中正确的是( )
当转台匀速转动时,用同种材料制成的a、b、c三个物体都相对于转台静止不动,如图所示.若ma=2mb=2mc,rc=2ra=2rb,则下列说法中正确的是( )
 当转台匀速转动时,用同种材料制成的a、b、c三个物体都相对于转台静止不动,如图所示.若ma=2mb=2mc,rc=2ra=2rb,则下列说法中正确的是( )
当转台匀速转动时,用同种材料制成的a、b、c三个物体都相对于转台静止不动,如图所示.若ma=2mb=2mc,rc=2ra=2rb,则下列说法中正确的是( )| A. | 物体a所受的静摩擦力大于c所受的静摩擦力 | |
| B. | 物体b所受的静摩擦力最小 | |
| C. | 物体c的向心加速度最小 | |
| D. | 转速缓慢增大时,物体a最先开始滑动 |
2.下列说法正确的是( )
| A. | 把金属块放在变化的磁场中可产生涡流 | |
| B. | 在匀强磁场中匀速运动的金属块会产生涡流 | |
| C. | 涡流对于生产和实验,既有有利的一面,也有不利的一面 | |
| D. | 大块金属中无感应电动势产生,直接产生了涡流 |
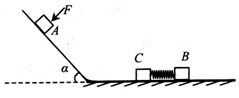 如图所示,粗糙的斜面与光滑的水平面通过半径可忽略的光滑小圆弧平滑连接.已知斜面的倾角α=45°,A、B、C是质量均为m=1kg的小滑块(均可视为质点),B和C用轻质弹簧连在一起.开始时,滑块B、C和弹簧均静止在水平面上.当滑块A置于斜面上且受到大小F=5$\sqrt{2}$N、方向垂直斜面向下的恒力作用时,恰能沿斜面向下匀速运动.现撤去F,让滑块A从斜面上距斜面底端L=10$\sqrt{2}$m处由静止下滑.取g=10m/s2.
如图所示,粗糙的斜面与光滑的水平面通过半径可忽略的光滑小圆弧平滑连接.已知斜面的倾角α=45°,A、B、C是质量均为m=1kg的小滑块(均可视为质点),B和C用轻质弹簧连在一起.开始时,滑块B、C和弹簧均静止在水平面上.当滑块A置于斜面上且受到大小F=5$\sqrt{2}$N、方向垂直斜面向下的恒力作用时,恰能沿斜面向下匀速运动.现撤去F,让滑块A从斜面上距斜面底端L=10$\sqrt{2}$m处由静止下滑.取g=10m/s2. 如图所示为固定在竖直平面内的轨道,直轨道AB与光滑圆弧轨道 BC相切,圆弧轨道的圆心角为37°,半径r=0.25m,C端水平,AB段的动摩擦因数为0.5.竖直墙壁CD高H=0.2m,紧靠墙壁在地面上固定一个和CD等高、底边长L=0.3m的斜面.一个质量m=0.1kg 的小物块(视为质点)在倾斜轨道上从距离B点l=0.5m处由静止释放,从C点水平抛出.重力加速度g=10m/s2,sin 37°=0.6,cos 37°=0.8.求:
如图所示为固定在竖直平面内的轨道,直轨道AB与光滑圆弧轨道 BC相切,圆弧轨道的圆心角为37°,半径r=0.25m,C端水平,AB段的动摩擦因数为0.5.竖直墙壁CD高H=0.2m,紧靠墙壁在地面上固定一个和CD等高、底边长L=0.3m的斜面.一个质量m=0.1kg 的小物块(视为质点)在倾斜轨道上从距离B点l=0.5m处由静止释放,从C点水平抛出.重力加速度g=10m/s2,sin 37°=0.6,cos 37°=0.8.求: