题目内容
如图所示，一个轻质直角形薄板ABC，AB=0.80m，AC=0.60m，在A点固定一垂直于薄板平面的光滑转动轴，在薄板上D点固定一个质量为m=0.40kg的小球，现用测力计竖直向上拉住B点，使AB水平，如图（a），测得拉力F1=2.0N；再用测力计竖直向上拉住C点，使AC水平，如图（b），测得拉力F2=2.0N（g取10m/s2，sin37°=0.6，cos37°=0.8）．求：（1）小球和转动轴的距离AD；
（2）在如图（a）情况下，将小球移动到BC边上距离A点最近处，然后撤去力F1，薄板转动过程中，AB边能转过的最大角度；
（3）在第（2）问条件下，薄板转动过程中，B点能达到的最大速度vB．
【答案】分析：（1）根据力矩平衡条件列式得到D点与AC边和AB边的间距，然后根据勾股定理求解AD间距；
（2）根据机械能守恒定律并结合对称性分析求解即可；
（3）根据机械能守恒定律列式求解出D点速度，求解出加速度，然后根据线速度和角速度、半径的关系式列式求解B点速度．
解答：解：（1）设小球D距AC为x，距AB为y．
AB边水平时，根据力矩平衡得：
AC边水平时，根据力矩平衡得：
所以
（2）设AD连线与AC边的夹角为θ，由几何关系可知θ=37°．根据机械能守恒定律得AD边转过的最大角度是2θ，所以AB边转过的最大角度是2θ=74°．
（3）根据机械能守恒定律，小球运动到最低点时，重力势能最小，动能最大
在转动过程中，薄板上各点角速度相同，所以
答：（1）小球和转动轴的距离AD为0.5m；
（2）AB边能转过的最大角度为74°；
（3）在第（2）问条件下，薄板转动过程中，B点能达到的最大速度为2.32m/s．
点评：本题关键是根据力矩平衡条件列式求解出D点的位置，然后根据机械能守恒定律或者动能定理列式求解．
（2）根据机械能守恒定律并结合对称性分析求解即可；
（3）根据机械能守恒定律列式求解出D点速度，求解出加速度，然后根据线速度和角速度、半径的关系式列式求解B点速度．
解答：解：（1）设小球D距AC为x，距AB为y．
AB边水平时，根据力矩平衡得：
AC边水平时，根据力矩平衡得：
所以
（2）设AD连线与AC边的夹角为θ，由几何关系可知θ=37°．根据机械能守恒定律得AD边转过的最大角度是2θ，所以AB边转过的最大角度是2θ=74°．
（3）根据机械能守恒定律，小球运动到最低点时，重力势能最小，动能最大
在转动过程中，薄板上各点角速度相同，所以
答：（1）小球和转动轴的距离AD为0.5m；
（2）AB边能转过的最大角度为74°；
（3）在第（2）问条件下，薄板转动过程中，B点能达到的最大速度为2.32m/s．
点评：本题关键是根据力矩平衡条件列式求解出D点的位置，然后根据机械能守恒定律或者动能定理列式求解．
练习册系列答案
小学生10分钟口算测试100分系列答案
相关题目
（2012?马鞍山模拟）如图所示，一个轻质光滑的滑轮（半径很小）跨在轻绳ABC上，滑轮下挂一个重为G的物体．今在滑轮上加一个水平拉力，使其向右平移到绳BC部分处于竖直、AB部分与天花板的夹角为60°的静止状态，则此时水平拉力的大小为（ ）
如图所示，一个轻质弹簧，固定于天花板的O点处，原长为L，一个质量为m的物块从A点竖直向上抛出，以速度v与弹簧在B点相接触，然后向上压缩弹簧，到C点时物块速度为零，在此过程中无机械能损失，则下列说法正确的是（ ）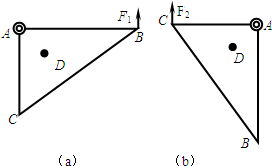
（2013?浦东新区一模）如图所示，一个轻质直角形薄板ABC，AB=0.80m，AC=0.60m，在A点固定一垂直于薄板平面的光滑转动轴，在薄板上D点固定一个质量为m=0.40kg的小球，现用测力计竖直向上拉住B点，使AB水平，如图（a），测得拉力F1=2.0N；再用测力计竖直向上拉住C点，使AC水平，如图（b），测得拉力F2=2.0N（g取10m/s2，sin37°=0.6，cos37°=0.8）．求：
)G B．(2＋
)G B．(2＋