题目内容
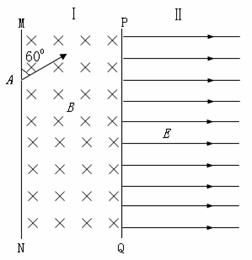
如图所示,在空间区域Ⅰ存在垂直纸面向里的磁感应强度为B=10T的匀强磁场,其边界为MN、PQ,其中PQ边界位置可以左右调节.在PQ右边空间区域Ⅱ存在水平向右的匀强电场,E= m/s其范围足够宽.在左边界的A点处有一个质量为m=1.0×10-12kg、带电量大小为q=1.0×10-13C的负电粒子,以速度V=3m/s沿着与左边界成60°的方向射入磁场,粒子重力不计,求:
m/s其范围足够宽.在左边界的A点处有一个质量为m=1.0×10-12kg、带电量大小为q=1.0×10-13C的负电粒子,以速度V=3m/s沿着与左边界成60°的方向射入磁场,粒子重力不计,求:(1)粒子在磁场中做圆周运动的半径
(2)若带电粒子从边界PQ飞出磁场,进入电场,经过一段时间,运动到电场中的C点,速度刚好减为零.求满足此种运动情况的磁场宽度以及粒子从A点到C点的时间;
(3)调节磁场与电场分界线PQ的位置,使粒子在磁场中运动的时间为t=
 π秒,恰好到达边界PQ时撤去磁场,同时将电场反向,粒子进入电场,经过一段时间到达D点,此时粒子速度方向与进入磁场时A点处的速度方向垂直,求粒子磁场中做圆周运动的圆心O点到D点的距离S.(结论可保留成根号形式)
π秒,恰好到达边界PQ时撤去磁场,同时将电场反向,粒子进入电场,经过一段时间到达D点,此时粒子速度方向与进入磁场时A点处的速度方向垂直,求粒子磁场中做圆周运动的圆心O点到D点的距离S.(结论可保留成根号形式)
【答案】分析:(1)粒子射入磁场中由洛伦兹力充当向心力,根据牛顿第二定律求解粒子圆周运动的半径;
(2)要使粒子运动到电场中的C点,速度刚好减为零,必须垂直PQ进入电场,画出粒子在磁场中运动的轨迹,由几何知识可求出磁场的宽度.由几何知识确定出粒子在磁场中运动时轨迹的圆心角,即可求出磁场中运动时间;根据牛顿第二定律和运动学公式结合可求出在电场中运动时间,即可求得总时间;
(3)根据t= ,确定出粒子在磁场中轨迹对应的圆心角为120°,可知,粒子速度沿PQ边界进入电场,在电场中粒子做类平抛运动,水平方向做匀加速运动,竖直方向做匀速直线运动,由牛顿第二定律和运动学公式结合求出水平和竖直位移,由几何知识求出的圆心O点到D点的距离S.
,确定出粒子在磁场中轨迹对应的圆心角为120°,可知,粒子速度沿PQ边界进入电场,在电场中粒子做类平抛运动,水平方向做匀加速运动,竖直方向做匀速直线运动,由牛顿第二定律和运动学公式结合求出水平和竖直位移,由几何知识求出的圆心O点到D点的距离S.
解答:解:(1)粒子在磁场中做匀速圆周运动,由牛顿第二定律得
qvB=m
解得 r=3m
(2)粒子飞出边界PQ时速度与PQ垂直,则磁场的宽度为
d=rsin30°=1.5m
粒子在磁场中运动的周期为T=
代入解得,T=2π (s)
粒子在磁场中运动时,速度的偏向角为30°,则轨迹对应的圆心也为30°,则粒子在磁场中运动的时间为 t1= T=
T= =
= s
s
粒子在电场中做匀减速直线运动,加速度为:a= m/s2
m/s2
由v=at2得,t2= =
=
故粒子从A点到C点的时间为t=t1+t2= s
s
(3)由题,粒子在磁场中运动的时间为t= π(s)=
π(s)= ,故圆心角θ=120°.
,故圆心角θ=120°.
所以粒子飞出磁场时,速度沿PQ边界,进入电场后做类平抛运动,水平方向做匀加速运动,竖直方向做匀速直线运动.
设粒子到达D点时,水平方向分速度大小为vy.
由题,粒子经过D点时速度方向与在A点时的速度方向垂直,由几何知识得:D点的速度与竖直方向的夹角为30°,则有
tan30°= =
=
解得,t= =1s
=1s
水平位移为 y= =
= m
m
竖直位移为 x=vt=3m
根据几何关系得:粒子磁场中做圆周运动的圆心O点到D点的距离S=
代入解得,S= m
m
答:
(1)粒子在磁场中做圆周运动的半径为3m;
(2)磁场宽度为1.5m,粒子从A点到C点的时间是 s;
s;
(3)粒子磁场中做圆周运动的圆心O点到D点的距离S是S= m.
m.
点评:本题是带电粒子在复合场中运动,分析运动情况时,要根据粒子的速度偏向角等于轨迹的圆心角,确定圆心角,画出轨迹.
(2)要使粒子运动到电场中的C点,速度刚好减为零,必须垂直PQ进入电场,画出粒子在磁场中运动的轨迹,由几何知识可求出磁场的宽度.由几何知识确定出粒子在磁场中运动时轨迹的圆心角,即可求出磁场中运动时间;根据牛顿第二定律和运动学公式结合可求出在电场中运动时间,即可求得总时间;
(3)根据t=
 ,确定出粒子在磁场中轨迹对应的圆心角为120°,可知,粒子速度沿PQ边界进入电场,在电场中粒子做类平抛运动,水平方向做匀加速运动,竖直方向做匀速直线运动,由牛顿第二定律和运动学公式结合求出水平和竖直位移,由几何知识求出的圆心O点到D点的距离S.
,确定出粒子在磁场中轨迹对应的圆心角为120°,可知,粒子速度沿PQ边界进入电场,在电场中粒子做类平抛运动,水平方向做匀加速运动,竖直方向做匀速直线运动,由牛顿第二定律和运动学公式结合求出水平和竖直位移,由几何知识求出的圆心O点到D点的距离S.解答:解:(1)粒子在磁场中做匀速圆周运动,由牛顿第二定律得
qvB=m

解得 r=3m
(2)粒子飞出边界PQ时速度与PQ垂直,则磁场的宽度为
d=rsin30°=1.5m
粒子在磁场中运动的周期为T=

代入解得,T=2π (s)
粒子在磁场中运动时,速度的偏向角为30°,则轨迹对应的圆心也为30°,则粒子在磁场中运动的时间为 t1=
 T=
T= =
= s
s粒子在电场中做匀减速直线运动,加速度为:a=
 m/s2
m/s2由v=at2得,t2=
 =
=
故粒子从A点到C点的时间为t=t1+t2=
 s
s(3)由题,粒子在磁场中运动的时间为t=
 π(s)=
π(s)= ,故圆心角θ=120°.
,故圆心角θ=120°.所以粒子飞出磁场时,速度沿PQ边界,进入电场后做类平抛运动,水平方向做匀加速运动,竖直方向做匀速直线运动.
设粒子到达D点时,水平方向分速度大小为vy.
由题,粒子经过D点时速度方向与在A点时的速度方向垂直,由几何知识得:D点的速度与竖直方向的夹角为30°,则有
tan30°=
 =
=
解得,t=
 =1s
=1s水平位移为 y=
 =
= m
m竖直位移为 x=vt=3m
根据几何关系得:粒子磁场中做圆周运动的圆心O点到D点的距离S=

代入解得,S=
 m
m答:
(1)粒子在磁场中做圆周运动的半径为3m;
(2)磁场宽度为1.5m,粒子从A点到C点的时间是
 s;
s;(3)粒子磁场中做圆周运动的圆心O点到D点的距离S是S=
 m.
m.点评:本题是带电粒子在复合场中运动,分析运动情况时,要根据粒子的速度偏向角等于轨迹的圆心角,确定圆心角,画出轨迹.

练习册系列答案
相关题目
 如图所示,在空间存在这样一个磁场区域,以MN为界,上部分的匀强磁场的磁感应强度为B1,下部分的匀强磁场的磁感应强度为B2,B1=2B2=2B0,方向均垂直纸面如图所示,且磁场区域足够大.在距离界线为h的某点有一带负电荷的A离子与一不带电的粒子B同时以某一速度以平行于界线MN的速度向右运动.粒子A质量为m,带电荷q,经过界线MN时的速度方向与界线成60°角进入下部分磁场.当粒子B沿与界线平行的直线到达位置Q点时(Q点在图中没有标出),恰好又与粒子A第一次相遇.不计A、B粒子的重力.求:
如图所示,在空间存在这样一个磁场区域,以MN为界,上部分的匀强磁场的磁感应强度为B1,下部分的匀强磁场的磁感应强度为B2,B1=2B2=2B0,方向均垂直纸面如图所示,且磁场区域足够大.在距离界线为h的某点有一带负电荷的A离子与一不带电的粒子B同时以某一速度以平行于界线MN的速度向右运动.粒子A质量为m,带电荷q,经过界线MN时的速度方向与界线成60°角进入下部分磁场.当粒子B沿与界线平行的直线到达位置Q点时(Q点在图中没有标出),恰好又与粒子A第一次相遇.不计A、B粒子的重力.求: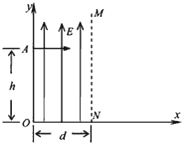 如图所示,在空间中取直角坐标系Oxy,在第一象限内平行于y轴的虚线MN与y轴距离为d,从y轴到MN之间的区域充满一个沿y轴正方向的匀强电场,场强大小为E.初速可忽略的电子经过一个电势差U未确定的电场直线加速后,从y轴上的A点以垂直于电场的方向射入第一象限区域,A点坐标为(0,h),已知电子的电量为e,质量为m,(重力忽略不计),若电子可以在第一象限从MN边界离开电场区域,求:
如图所示,在空间中取直角坐标系Oxy,在第一象限内平行于y轴的虚线MN与y轴距离为d,从y轴到MN之间的区域充满一个沿y轴正方向的匀强电场,场强大小为E.初速可忽略的电子经过一个电势差U未确定的电场直线加速后,从y轴上的A点以垂直于电场的方向射入第一象限区域,A点坐标为(0,h),已知电子的电量为e,质量为m,(重力忽略不计),若电子可以在第一象限从MN边界离开电场区域,求: 如图所示,在空间区域Ⅰ存在垂直纸面向里的磁感应强度为B=10T的匀强磁场,其边界为MN、PQ,其中PQ边界位置可以左右调节.在PQ右边空间区域Ⅱ存在水平向右的匀强电场,E=
如图所示,在空间区域Ⅰ存在垂直纸面向里的磁感应强度为B=10T的匀强磁场,其边界为MN、PQ,其中PQ边界位置可以左右调节.在PQ右边空间区域Ⅱ存在水平向右的匀强电场,E=