题目内容

质量为1×103 kg的汽车，发动机输出功率为3.0×103 W，在水平公路上能达到的最大速度为15m/s，当汽车的速度为10m/s时，其加速度为
0.1
0.1
m/s2．
分析：当牵引力等于阻力时，速度最大，根据最大速度和输出功率求出阻力的大小，再根据P=Fv求出速度为10m/s时汽车的牵引力，根据牛顿第二定律求出汽车的加速度．
解答：解：解：设汽车所受阻力为Ff，当牵引力等于阻力时，速度最大．
有：P0=Ffvm得：Ff=
P0
vm
=
3.0×103
15
N=200N
当速度为10m/s时的牵引力为：F=
P0
v
=
3.0×103
15
N=300N
由牛顿第二定律得：F-Ff=ma
即加速度为：a=
F-Ff
m
=
300-200
1000
m/s2=0.1m/s2
故答案为：0.1．
点评：解决本题的关键知道发动机的输出功率与牵引力的关系，以及知道当牵引力等于阻力时，速度最大．
练习册系列答案
相关题目
（2008?东城区三模）（1）在“验证机械能守恒定律”的实验中，打点计时器接在电压为E，频率为f，的交流电源上，在实验中打下一条理想纸带，如图1所示，选取纸带上打出的连续5个点A、B、C、D、E，测出A点距起始点的距离为s0，点AC间的距离为s1，点CE间的距离为s2，已知重锤的质量为m，当地的重力加速度为g，则：

①从起始点O到打下C点的过程中，重锤重力势能的减少量为△EP=
mg（S0+S1）
mg（S0+S1）
，重锤动能的增加量为△EK
m(s1+s2)2f2
32
m(s1+s2)2f2
32
．
②根据题中提供的条件，可求出重锤实际下落的加速度a=
(s2-s1)f2
4
(s2-s1)f2
4
，它和当地的重力加速度g进行比较，则a
小于
小于
g（填大于，等于，小于）．
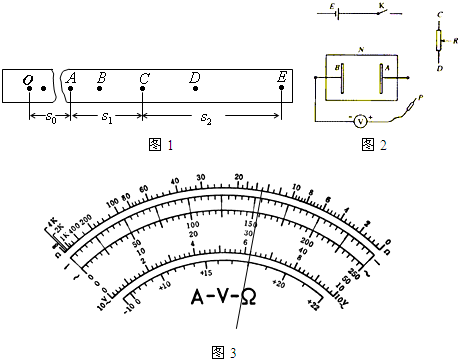
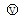（2）如图2给出器材为：电源E（电动势为12V，内阻不计），木板N（板上从下往上依次叠放白纸、复写纸、导电纸各一张），两个金属条A、B（平行放置在导电纸上，与导电纸接触良好，用作电极），滑线变阻器R（其总阻值小于两平行电极间导电纸的电阻），直流电压表（量程为6V，内阻很大，其负接线柱与B极相连，正接线柱与探针P相连），开关K．现要用图中仪器描绘两平行金属条AB间电场中的等势线．AB间的电压要求取为6V．
（Ⅰ）在图2中连线，画成实验电路原理图．
（Ⅱ）下面是主要的实验操作步骤，将所缺的内容填写在横线上方．
a．接好实验电路．
b．
把变阻器的滑动触头移到靠近D端处
把变阻器的滑动触头移到靠近D端处
．
c．合上K，并将探针P与A相接触．
d．
调节R，使电压表读数为6V
调节R，使电压表读数为6V
．
e．用探针压印的方法把A、B的位置标记在白纸上．画一线段连接AB两极，在连线上选取间距大致相等的5个点作为基准点，用探针把它们的位置印在白纸上．
f．将探针与某一基准点相接触，
记下电压表读数，在导电纸上移动探针，找出电压表读数与所记下的数值相同的另一点
记下电压表读数，在导电纸上移动探针，找出电压表读数与所记下的数值相同的另一点
，这一点是此基准的等势点．用探针把这一点的位置也压印在白纸上．用相同的方法找出此基准点的其它等势点．
g．重复步骤f，找出其它4个基准点的等势点．取出白纸画出各条等势线．
（3）如图3是多用表的刻度盘，当选用量程为50mA的电流档测量电流时，表针指于图示位置，则所测电流为
30.7
30.7
mA；若选用倍率为“×100”的电阻档测电阻时，表针也指示在图示同一位置，则所测电阻的阻值为
1.5×103
1.5×103
Ω．如果要用此多用表测量一个约2.0×104Ω的电阻，为了使测量比较精确，应选的欧姆档是
×1K
×1K
（选填“×10”、“×100”或“×1K”）．换档结束后，实验操作上首先要进行的步骤是
欧姆调零．
欧姆调零．
．
“和平号”空间站已于2001年3月23日成功地坠落在太平洋海域，坠落过程可简化为从一个近圆轨道（可近似看作圆轨道）开始，经过与大气摩擦，空间站的绝大部经过升温、熔化，最后汽化而销毁，剩下的残片坠入大海.此过程中，空间站原来的机械能中，除一部分用于销毁和一部分被残片带走外，还有一部分能量E′通过其他方式散失（不考虑坠落过程中发生化学反应所需的能量）.

（1）试用以下各物理量的符号表示散失能量E′的公式；

（2）根据下列数据，算出E′的数值.（结果保留两位有效数字）坠落开始时，空间站的质量m0=1.17×105 kg；

轨道距地面的高度为h=146 km;

地球半径R=6.4×106 m；

坠落空间范围内重力加速度取g=10 m/s2;

入海残片的质量为m=1.2×104 kg;

入海残片的温度升高Δt=3 000 K；

入海残片的入海速度为声速v=340 m/s;

空间站材料每千克升温1 K平均所需能量C=1.0×103 J；

每销毁1 kg材料平均所需能量μ=1.0×107 J

一台二氧化碳激光器发出的激光功率为P=1 000 W，出射光束截面积为A=1 mm2,这束光垂直射到温度为T=273 K，厚度为d=2 cm的铁板上，如果有80%的光束能量被激光照射到那一小部分铁板所吸收，并使其熔化成与光束等截面积的直圆柱孔，需要多少时间？铁的有关参数：热容量c=26.6 J/mol·K，密度ρ=7.90×103 kg/m3,熔点Tm=1 798 K,熔解热L=1.49×104 J/mol,摩尔质量U=56×10-3 kg。

如图所示，一个上下都与大气相通的直圆筒，内部横截面积为S = 0.01m2，中间用两个活塞A和B封住一定质量的气体。A、B都可沿圆筒无摩擦地上下滑动，且不漏气。A的质量不计，B的质量为M，并与一劲度系数为k = 5×103 N/m的较长的弹簧相连。已知大气压p0= 1×105 Pa，平衡时两活塞之间的距离l0 = 0.6 m，现用力压A，使之缓慢向下移动一段距离后，保持平衡。此时用于压A的力F = 500 N。求活塞A下移的距离。

 

如图所示，一个上下都与大气相通的直圆筒，内部横截面积为S = 0.01m2，中间用两个活塞A和B封住一定质量的气体。A、B都可沿圆筒无摩擦地上下滑动，且不漏气。A的质量不计，B的质量为M，并与一劲度系数为k = 5×103 N/m的较长的弹簧相连。已知大气压p0 = 1×105 Pa，平衡时两活塞之间的距离l0 = 0.6 m，现用力压A，使之缓慢向下移动一段距离后，保持平衡。此时用于压A的力F = 500 N。求活塞A下移的距离。

 

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网