题目内容
将倾角为θ的足够长的光滑绝缘斜面放在范围足够大的磁感应强度为B的匀强磁场中，一个质量为m，电荷量为q的带电体沿斜面由静止开始下滑，如图所示．滑到某一位置开始离开斜面．问：（1）物体带何种电荷？
（2）物体刚离开斜面时的速度多大？
（3）斜面长度至少为多少？
分析：带电物体下滑到某一位置离开斜面，由此可知洛伦兹力垂直于斜面向上，根据左手定则判断带电物体的电性．
对物体进行受力分析，当物体对斜面的压力为零时，物体开始离开斜面，由平衡条件求出物体此时的速度；
由牛顿第二定律求出物体的加速度，然后由匀变速运动的速度位移公式求出物体在斜面上滑行的长度．
对物体进行受力分析，当物体对斜面的压力为零时，物体开始离开斜面，由平衡条件求出物体此时的速度；
由牛顿第二定律求出物体的加速度，然后由匀变速运动的速度位移公式求出物体在斜面上滑行的长度．
解答：解：（1）根据题意由左手定则可得粒子带负电．
（2）由题可知粒子刚离开斜面时有：
qvB=mgcosθ
解得物体离开斜面时的速度为：v=
（3）设物体下滑距离为S时则好离开斜面，由动能定理有：
mgssinθ=
mV2
解得：x=
则斜面长度至少为：x=
答：（1）物体带负电荷；
（2）物体刚离开斜面时的速度为
；
（3）斜面长度至少为
．
（2）由题可知粒子刚离开斜面时有：
qvB=mgcosθ
解得物体离开斜面时的速度为：v=
| mgcosθ |
| qB |
（3）设物体下滑距离为S时则好离开斜面，由动能定理有：
mgssinθ=
| 1 |
| 2 |
解得：x=
| m2gcos2θ |
| 2q2B2sinθ |
则斜面长度至少为：x=
| m2gcos2θ |
| 2q2B2sinθ |
答：（1）物体带负电荷；
（2）物体刚离开斜面时的速度为
| mgcosθ |
| qB |
（3）斜面长度至少为
| m2gcos2θ |
| 2q2B2sinθ |
点评：解决本题的关键是正确地进行受力分析，抓住垂直于斜面方向上的合力为零时，物体开始离开斜面进行分析求解．
练习册系列答案
全优点练单元计划系列答案
相关题目
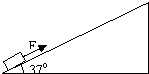如图所示，在倾角为θ=37°的足够长的固定足够长的斜面底端有一质量为m=2kg的物体，物体与斜面间动摩擦因数为μ=0.25．现用轻细绳将物体由静止沿斜面向上拉动，拉力F=20N，方向平行斜面向上．经时间t1=4s绳子突然断裂，求：（sin37°=0.6，cos37°=0.8，g=10m/s2）
。烧断两滑块间的轻质绳后，由于弹簧弹力的作用，滑块A将沿圆轨道做圆周运动，且在最高点P轨道对滑块的压力恰好等于滑块的重力。已知两滑块的质量之比为
，重力加速度g=10m/s2.求：
