题目内容
16.一个带电粒子在洛伦兹力的作用下做匀速圆周运动,要想确定该带电粒子的比荷(粒子的电量与质量之比),则只需要知道( )| A. | 运动速度v和磁感应强度B | B. | 磁感应强度B和运动周期T | ||
| C. | 轨迹半径r和运动速度v | D. | 轨迹半径r和磁感应强度B |
分析 带电粒子在磁场力的作用下做圆周运动洛伦兹力做为向心力,根据向心力的公式来分析比荷.
解答 解:带电粒子在匀强磁场中做匀速圆周运动,洛伦兹力提供向心力,由牛顿第二定律得:qvB=m$\frac{{v}^{2}}{r}$,
得:$r=\frac{mv}{qB}$
解得:T=$\frac{2πr}{v}=\frac{2πm}{qB}$,
所以:$\frac{q}{m}=\frac{2π}{BT}$,或$\frac{q}{m}=\frac{v}{Br}$,
由此可知,求比荷需要知道粒子的线速度、磁感应强度、轨道半径,或磁感应强度、周期,
故ACD错误,B正确;
故选:B.
点评 该题考查带电粒子在匀强磁场中的运动,根据带电粒子在磁场中做圆周运动的半径周期公式可以快速的作出判断,所以掌握住结论有利于提高解题的速度.

练习册系列答案
相关题目
6.如图所示,物块静止在固定的斜面上,则下列说法中正确的是( )


| A. | 物体受到弹力和重力的合力为零 | |
| B. | 物体受到弹力和摩擦力的合力为零 | |
| C. | 物体受到弹力的方向垂直斜面向下 | |
| D. | 物体受到摩擦力和重力的合力方向垂直斜面向下 |
7.下列措施可以防止静电危害的是( )
| A. | 电工钳柄上套有绝缘胶套 | B. | 飞机的机轮上装有搭地线 | ||
| C. | 在高大的烟囱中安装静电除尘器 | D. | 印染车间中保持适当的湿度 |
4. 静电喷涂时,喷枪带负电,被喷工件带正电,喷枪喷出的涂料微粒带负电,假设微粒被喷出后只受静电力作用,最后吸附在工件表面,微粒在向工件靠近的过程中( )
静电喷涂时,喷枪带负电,被喷工件带正电,喷枪喷出的涂料微粒带负电,假设微粒被喷出后只受静电力作用,最后吸附在工件表面,微粒在向工件靠近的过程中( )
 静电喷涂时,喷枪带负电,被喷工件带正电,喷枪喷出的涂料微粒带负电,假设微粒被喷出后只受静电力作用,最后吸附在工件表面,微粒在向工件靠近的过程中( )
静电喷涂时,喷枪带负电,被喷工件带正电,喷枪喷出的涂料微粒带负电,假设微粒被喷出后只受静电力作用,最后吸附在工件表面,微粒在向工件靠近的过程中( )| A. | 一定沿着电场线运动 | B. | 所受电场力先减小后增大 | ||
| C. | 克服电场力做功 | D. | 电势能逐渐增大 |
1.一质点沿直线运动时的v-t图象如图所示,以下说法中正确的是( )


| A. | 第2s末质点的速度方向发生改变 | B. | 第3s内质点的加速度大小为$\frac{2}{3}$m/s2 | ||
| C. | 第2s末和第4s末质点的位置相同 | D. | 前6s内质点的位移为8m |
8.根据最新官方消息,中国火星探测任务基本确定,发射时间大致在2018年左右,若火星探测器在登陆火星之前需在靠近火星表面绕火星做匀速圆周运动,已知引力常量为G,探测器在火星表面附近绕火星做匀速圆周运动的角速度为ω,则火星的平均密度为( )
| A. | $\frac{3{ω}^{2}}{4πG}$ | B. | $\frac{2{ω}^{2}}{3πG}$ | C. | $\frac{{ω}^{2}}{2πG}$ | D. | $\frac{{ω}^{2}}{4πG}$ |
5. 如图所示,水平固定一截面为正方形绝缘方管的长度为L,空间存在场强为E、方向水平向右的匀强电场和磁感应强度为B.方向竖直向下的匀强磁场,将质量为m、带电量为+q的小球从左侧管口无初速度释放,已知小球与管道各接触面间动摩擦因数均为μ,小球运动到右侧管口处时速度为v,该过程( )
如图所示,水平固定一截面为正方形绝缘方管的长度为L,空间存在场强为E、方向水平向右的匀强电场和磁感应强度为B.方向竖直向下的匀强磁场,将质量为m、带电量为+q的小球从左侧管口无初速度释放,已知小球与管道各接触面间动摩擦因数均为μ,小球运动到右侧管口处时速度为v,该过程( )
 如图所示,水平固定一截面为正方形绝缘方管的长度为L,空间存在场强为E、方向水平向右的匀强电场和磁感应强度为B.方向竖直向下的匀强磁场,将质量为m、带电量为+q的小球从左侧管口无初速度释放,已知小球与管道各接触面间动摩擦因数均为μ,小球运动到右侧管口处时速度为v,该过程( )
如图所示,水平固定一截面为正方形绝缘方管的长度为L,空间存在场强为E、方向水平向右的匀强电场和磁感应强度为B.方向竖直向下的匀强磁场,将质量为m、带电量为+q的小球从左侧管口无初速度释放,已知小球与管道各接触面间动摩擦因数均为μ,小球运动到右侧管口处时速度为v,该过程( )| A. | 洛伦兹力对小球做功为$\frac{1}{2}$qvBL | |
| B. | 电场力对小球做功为qEL | |
| C. | 系统因摩擦而产生的热量为μmgL | |
| D. | 系统因摩擦而产生的热量为qEL-$\frac{1}{2}$mv2 |
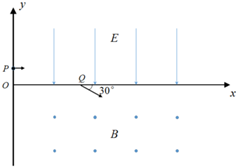 如图所示的xoy坐标系中,在第Ⅰ象限内存在沿y轴负向的匀强电场,第Ⅳ象限内存在垂直纸面向外的匀强磁场,一质量为m、电荷量为q的带正电粒子,从y轴上的P点垂直进入匀强电场,经过x轴上的Q点以速度v进入磁场,方向与x轴正向成30°.若粒子在磁场中运动后恰好能再回到电场,已知$\overrightarrow{OQ}$=3L,粒子的重力不计,电场强度E和磁感应强度B大小均求知,求
如图所示的xoy坐标系中,在第Ⅰ象限内存在沿y轴负向的匀强电场,第Ⅳ象限内存在垂直纸面向外的匀强磁场,一质量为m、电荷量为q的带正电粒子,从y轴上的P点垂直进入匀强电场,经过x轴上的Q点以速度v进入磁场,方向与x轴正向成30°.若粒子在磁场中运动后恰好能再回到电场,已知$\overrightarrow{OQ}$=3L,粒子的重力不计,电场强度E和磁感应强度B大小均求知,求
